Modelos probabilísticos y determinísticos para toma de decisiones y administración de empresas
Modelos probabilísticos y determinísticos para toma de decisiones y administración de empresas
Oscar Antonio Robles Villanueva, Mariel Del Rocío Chotón Calvo, María Silvia Villa Santillan, Ricardo Antonio Armas Juarez, Mariela Lizety Cordova Espinoza, Ricardo Martin Gomez Arce
© Oscar Antonio Robles Villanueva, Mariel Del Rocío Chotón Calvo, María Silvia Villa Santillan, Ricardo Antonio Armas Juarez, Mariela Lizety Cordova Espinoza, Ricardo Martin Gomez Arce, 2024
Primera edición: Julio, 2024
Editado por:
Editorial Mar Caribe
Av. General Flores 547, Colonia, Colonia-Uruguay.
RUC: 15605646601
Diseño de cubierta: Yelitza Sánchez Cáceres
Libro electrónico disponible en https://editorialmarcaribe.es/modelos-probabilisticos-y-deterministicos-para-toma-de-decisiones-y-administracion-de-empresas/
Formato: electrónico
ISBN: 978-9915-9682-4-7
Aviso de derechos de atribución no comercial: Los autores pueden autorizar al público en general a reutilizar sus obras únicamente con fines no lucrativos, los lectores pueden usar una obra para generar otra obra, siempre y cuando se dé el crédito de investigación y, otorgan a la editorial el derecho de publicar primero su ensayo bajo los términos de la licencia CC BY-NC 4.0.
ÍNDICE
1. LA INVESTIGACIÓN DE OPERACIONES.
1.1 Modelos de la Investigación de Operaciones.
La necesidad de una escala numérica y mesurable.
Clasificación de las características.
1.2 La Modelización en la toma de Decisiones.
1.4 Algunas diferencias entre el Diseño y la Materialización del Modelo.
1.5 Elementos Estructurado para la toma de Decisiones.
Estructuración del Proceso de Toma de Decisiones.
1.6 Las limitaciones de la Naturaleza Humana.
1.7 Diagramas Causales o de Lazos.
1.8 Modelo Migración Población, Migración, Empleo.
1.9 Relaciones Causa-Efecto Modelos de Aplicación.
Población Empleada Positivo. Lazo Migración
1.10 Modelo de la Oferta con retardo.
EL PROCESO DE TOMA DE DECISIONES ANTE SITUACIONES QUE IMPLICAN RIESGO E INCERTIDUMBRE.
Exactitud del Modelo Estadístico.
2.1. De los datos a un conocimiento decisivo.
2.2 Toma de Decisiones Estadística.
Estrategias para la toma de Decisiones.
2.3 Proceso de Toma de Decisiones.
2.4 Modelos de Decisión Estocásticos.
Elementos de un Modelo Probabilístico.
La Relevancia de la Información disminuye la Incertidumbre.
2.6 Tomar Decisiones en la Incertidumbre
2.7 Consideración de los Riesgos.
2.8 Respuestas con respecto al riesgo y su impacto.
2.9 Cuando se Evalúa el Riesgo,
2.10 Análisis de Dos Inversiones.
2.11 El Árbol de Decisiones y la Matriz.
Árbol de decisión reducido para ABC
Valor esperado en función de P(S)
3.1 Determinación de la región Factible.
3.5 Características de las Operaciones Deterministas.
3.7 características del Modelo M/M/S
Figura 3.1 se representa el Modelo
3.9 Modelo y análisis del Sistema de Cola Actual.
Rendimiento obtenidas con Queuing Analysis „ en el WinQSB .
4.1 La Administración de Proyectos.
4.2 La Situación Probabilística.
4.3 Análisis de las Probabilidades.
PRÓLOGO
Un enfoque progresivo del modelado es esencial en el proceso de toma de decisiones. Este enfoque involucra a dos partes clave: quien toma las decisiones y quien construye el modelo, a quien a menudo se le llama analista. El analista juega un papel crucial al ayudar a quien toma las decisiones durante todo el proceso de toma de decisiones. Para cumplir eficazmente este papel, el analista debe poseer algo más que un conjunto de métodos analíticos; también deben poseer una comprensión integral del proceso de toma de decisiones. El análisis de decisiones ofrece una herramienta valiosa para quienes EMITEN fallos en una amplia gama de campos, incluidos ingenieros, planificadores, agencias públicas, gerentes de proyectos, analistas financieros y expertos en diversas disciplinas médicas y tecnológicas.
Su soporte cuantitativo permite a estos profesionales tomar decisiones informadas en sus respectivas áreas de especialización. En el campo de la construcción de modelos, los expertos a menudo se sienten atraídos por investigar a fondo un problema antes de retirarse a sus propias mentes para construir un modelo matemático para que lo utilice el gerente o la persona que toma las decisiones, surge un desafío importante cuando el gerente carece de una comprensión completa de las complejidades del modelo. Esto podría dar como resultado que el gerente implemente ciegamente el modelo sin comprender sus principios subyacentes o lo rechace rotundamente. Esta desconexión entre el especialista y el gerente a veces puede generar una sensación de frustración en ambas partes. El especialista puede percibir que el gerente está alarmantemente desinformado y carente de sofisticación al intentar evaluar el modelo, mientras que el gerente puede considerar que el especialista habita en un mundo de suposiciones poco prácticas y utiliza una jerga matemática compleja que parece irrelevante para el escenario del mundo real en cuestión.
Estos desafíos de malentendidos y comunicación ineficaz pueden evitarse si el gerente colabora estrechamente con el especialista en el desarrollo de un modelo básico que ofrezca un análisis aproximado pero comprensible. Una vez que el gerente se sienta cómodo con el modelo, se pueden incorporar gradualmente y con cautela más detalles y una mayor sofisticación. Este procedimiento exige la inversión de tiempo del administrador y el compromiso genuino del analista para resolver los problemas reales del administrador, en lugar de intentar crear y explicar modelos excesivamente complejos. Esta construcción gradual del modelo, a menudo conocida como enfoque de arranque, es el determinante clave de un modelo de decisión de implementación exitoso, el enfoque de arranque simplifica las complejidades involucradas en la validación y verificación del modelo. Un sistema puede definirse como un conjunto de componentes interconectados que funcionan juntos de manera coordinada para lograr un objetivo específico. Es la interdependencia y la interacción entre estos componentes lo que en última instancia determina el funcionamiento general y el propósito del sistema. En consecuencia, las relaciones y conexiones dentro del sistema suelen tener mayor importancia que los componentes individuales por sí solos. Además, cuando los sistemas se construyen combinando unidades o subsistemas más pequeños, se les denomina subsistemas dentro del sistema más grande. La dinámica de un sistema: un sistema que permanece sin cambios se considera estático o determinista. Sin embargo, la mayoría de los sistemas que encontramos son de naturaleza dinámica, lo que significa que sufren cambios con el tiempo, estos cambios se basan en el comportamiento exhibido por el sistema.
Si el sistema sigue un patrón de desarrollo predecible, nos referimos a él como si tuviera un patrón de comportamiento. El hecho de que un sistema sea estático o dinámico depende del marco temporal de estudio y de las variables específicas que son el foco del análisis. El horizonte temporal se refiere al tiempo durante el cual se observa y examina el sistema, mientras que las variables son los valores ajustables dentro del sistema. En los modelos deterministas, la evaluación de la calidad de una decisión se basa únicamente en sus resultados. Sin embargo, en los modelos probabilísticos la evaluación del directivo va más allá de los resultados y también toma en consideración el nivel de incertidumbre o riesgo asociado a cada decisión. Para ilustrar la distinción entre modelos probabilísticos y deterministas, consideremos los reinos del pasado y el futuro.
Cuando se trata del pasado, sin importar nuestras acciones en el presente, no podemos alterar lo que ya ocurrió. Por otro lado, cuando nos centramos en el futuro, nuestras elecciones y decisiones tienen la capacidad de ejercer influencia y provocar cambios, aunque siga existiendo un cierto nivel de incertidumbre. Como directivos, a menudo nos sentimos cautivados por la oportunidad de dar forma al futuro, dándole mayor importancia que el análisis y la insistencia en acontecimientos pasados. El concepto de probabilidad ocupa un lugar importante en el proceso de toma de decisiones, ya sea dentro de una empresa, el gobierno, las ciencias sociales o nuestra vida cotidiana. Es raro tener toda la información necesaria disponible al tomar decisiones, y la mayoría de las decisiones se toman en medio de la incertidumbre.
A diferencia de los procesos de toma de decisiones determinísticas tal como, optimización lineal resuelta mediante sistema de ecuaciones, sistemas paramétricos de ecuaciones y en la toma de decisión bajo pura incertidumbre, las variables son normalmente más numerosas y por lo tanto más difíciles de medir y controlar, los pasos para resolverlos son los mismos. El modelo es una representación simplificada de la situación real, no necesita estar completo o exacto en todas las relaciones. Este se entiende con mayor facilidad que un suceso empírico (observado), por lo tanto permite que el problema sea resuelto con mayor facilidad y con un mínimo de esfuerzo y pérdida de tiempo. El modelo puede usarse repetidamente para problemas similares, y además puede ajustarse y modificarse, afortunadamente, los métodos probabilísticos y estadísticos para analizar la toma de decisiones en condiciones de incertidumbre son mucho más numerosos y poderosos que nunca. Las computadoras ofrecen muchos usos prácticos. Algunos ejemplos de aplicaciones comerciales son los siguientes: Un auditor puede utilizar técnicas de muestreo aleatorio para auditar las cuentas por cobrar de un cliente. Un gerente de planta puede utilizar técnicas de control de calidad para asegurar la calidad de los productos con mínima inspección y menor número de pruebas. Un analista financiero podría usar métodos de regresión y evaluación para entender mejor la analogía entre los indicadores financieros y un conjunto de otras variables de negocio. Un analista de mercado podría usar pruebas de significancia para aceptar o rechazar una hipótesis sobre un grupo de posibles compradores a los cuales la compañía está interesada en vender sus productos, un gerente de ventas podría usar técnicas para predecir las ventas de los próximos períodos.
CAPÍTULO I
MODELOS PROBABILÍSTICOS
1. LA INVESTIGACIÓN DE OPERACIONES.
La investigación de operaciones ha demostrado ser exitosa en muchas organizaciones, pero todavía hay escépticos que no reconocen su valor, para abordar esto es necesario un cambio en la forma de enseñar y presentar la Investigación Operativa, enfatizando su aplicación práctica en las organizaciones. A los directivos, que estaban más alejados de las matemáticas en el aula que los investigadores, les resultó difícil aplicar estos algoritmos en situaciones de toma de decisiones de la vida real, la solución manual de un problema de decisión mediante un algoritmo Simplex puso de relieve la dificultad del proceso, la baja relación costo/beneficio y la complejidad de las situaciones de la vida real hicieron que los gerentes prefirieran criterios más heurísticos y descartaran los enfoques matemáticos. Esto resultó en una división entre la toma de decisiones y la ciencia y la tecnología. La investigación de operaciones, también conocida como ciencia de la gestión, ha sido un campo bien establecido durante más de un siglo y sus orígenes se remontan a principios del siglo XX.
Su prominencia alcanzó su punto máximo al final de la Segunda Guerra Mundial, cuando el mundo experimentaba una rápida industrialización y una alta demanda. A medida que las técnicas de investigación de operaciones se aplicaron a las organizaciones, el campo se expandió más allá de los matemáticos e ingenieros para incluir profesionales en administración y economía, a medida que los escenarios económicos globales cambiaron (pasando de una economía basada en la oferta a una basada en la demanda) y entraron en juego factores adicionales (como la introducción de más restricciones y criterios de decisión más allá del costo), la efectividad de estos algoritmos comenzó a disminuir ser cuestionado.
Esta división hizo que los profesionales de la gestión, especialmente los administradores, perdieran valiosas herramientas para la toma de decisiones. Sin embargo, la revolución informática cerró esta brecha al permitir que las metodologías y el software matemáticos fueran accesibles para los usuarios. Las computadoras permitieron la integración de la ciencia con la toma de decisiones, permitiendo a los gerentes utilizar enfoques matemáticos y evaluar resultados basados en su conocimiento de la situación. En pocas palabras, la Investigación de Operaciones se basa en dos premisas fundamentales: enseñar a las personas cómo modelar y pensar sistémicamente sobre una situación y proporcionarles una variedad de herramientas informáticas para ayudar a encontrar soluciones, si bien no pretende ser original en su contenido teórico debido a la gran cantidad de literatura existente sobre el tema, pretende recopilar diversos artículos, trabajos y notas.
Muchos de estos recursos provienen de la fascinante aldea global de Internet. Considero que la Investigación Operativa es una herramienta vital para la toma de decisiones, particularmente para los estudiantes de administración. Son los actores principales que entienden los entresijos de una organización o de su área específica. Es fundamental involucrar a los tomadores de decisiones en la construcción del modelo para asegurar su uso efectivo. La Investigación de Operaciones no se limita a matemáticos o informáticos; es un campo dinámico y apasionante dentro de la gestión organizacional donde los futuros profesionales prosperarán. Durante este tiempo, la atención se centró en encontrar soluciones para sistemas militares complejos y empresas que tomaban decisiones basándose únicamente en los costos.
El mercado pudo absorber importantes volúmenes de producción, lo que permitió el desarrollo de técnicas y algoritmos matemáticos para resolver problemas con diversas restricciones. Estas técnicas fueron ampliamente aceptadas y exitosas en el entorno económico de la época. Un ejemplo notable es el método Simplex, que fue desarrollado por G. Dantzing en 1947, este restableció la importancia de la Investigación Operativa en la gestión, ofreciendo herramientas para ayudar a la toma de decisiones con rapidez y sencillez, destacó que la preparación e interpretación del modelo siguen siendo tareas cruciales para quien toma las decisiones.
La investigación de operaciones, también conocida como IO, es un campo que se centra en la resolución de problemas y la toma de decisiones dentro de las organizaciones, abarca una amplia gama de industrias, incluidas la manufactura, el transporte, las telecomunicaciones, las finanzas, la atención médica y el ejército, la IO utiliza un enfoque científico similar a los campos científicos establecidos, utilizando observación cuidadosa, recopilación de datos y la construcción de modelos matemáticos para representar problemas del mundo real. Luego, estos modelos se prueban mediante experimentos para validar su precisión y eficacia I no sólo implica investigación e investigación científica, sino también administración práctica y proporcionar conclusiones claras para los tomadores de decisiones.
Se necesita un punto de vista organizacional, con el objetivo de resolver conflictos de intereses y lograr los mejores resultados para toda la organización, uno de los objetivos clave de la IO es encontrar soluciones óptimas para los problemas actuales, considerando varios factores y perspectivas. Debido a la complejidad y la naturaleza multidisciplinaria de la IO, requiere la experiencia de personas de diversos orígenes, incluidas matemáticas, estadística, economía, administración de empresas, informática, ingeniería, ciencias físicas y ciencias del comportamiento. La colaboración de equipos interdisciplinarios es esencial para la resolución integral de problemas y considerar todas las implicaciones del problema en toda la organización. La definición internacionalmente aceptada de IO enfatiza su aplicación de métodos científicos a problemas complejos en la gestión de grandes sistemas, incorporando mediciones de factores como el cambio y el riesgo para predecir y comparar decisiones, estrategias o controles alternativos. En última instancia, el propósito de la IO es ayudar a la gerencia a formular políticas y acciones informadas y respaldadas científicamente.
1.1 Modelos de la Investigación de Operaciones.
Un enfoque sistemático para la resolución de problemas, con un enfoque en colaborar como equipo para aprovechar la experiencia de los especialistas de IO en la evaluación, coordinación e incorporación de conocimientos relevantes proporcionados por expertos en otros campos, todo con el objetivo de resolver un problema específico. problema (también conocido como enfoque de grupo de expertos). El proceso de modelado estructurado juega un papel central en la investigación de operaciones, sirviendo como actividad principal. Esto nos lleva a preguntarnos si el modelo representa con precisión el mundo real, si bien el modelo no es un reflejo directo de la realidad, sí incorpora ciertos elementos. Esto plantea otra pregunta importante: ¿incluye el modelo las partes relevantes necesarias para resolver el problema de decisión en cuestión? El razonamiento y los cálculos simbólicos son fundamentales en el proceso de modelado analítico, al igual que en matemáticas.
Por lo tanto, al igual que cuando se aprende un idioma extranjero, es necesario desarrollar una comprensión de las matemáticas, ya que es el lenguaje de todas las ciencias, incluido el proceso de modelado en IO, cuyo objetivo es ayudar a los tomadores de decisiones. Un modelo mental representa los pensamientos de quien toma decisiones con respecto a la realidad, esencialmente exteriorizando su percepción, los matemáticos utilizan símbolos y notaciones, incluidos números, para crear modelos, así, tenemos tres conceptos distintos: la realidad, el modelo mental y su representación. En todas sus formas, el modelado analítico es un proceso de pensamiento estructurado que implica reconocer y articular un problema, y posteriormente cuantificarlo traduciendo palabras en expresiones matemáticas, el modelado sirve como un proceso de pensamiento enfocado y secuencial que ayuda a comprender los problemas de decisión.
Al adoptar un enfoque científico, los administradores pueden hacer predicciones precisas incluso en situaciones sobre las que no tienen control total, la información cualitativa se puede caracterizar y procesar mediante asignación numérica, utilizamos varias escalas numéricas y mensurables para cuantificar el mundo. Podemos obtener una comprensión del mundo identificando relaciones y utilizando manipulación, comparación, cálculo y otros métodos, y luego usando las mismas escalas para adaptar nuestros hallazgos al mundo real.
Gráfico 1.1
La necesidad de una escala numérica y mesurable.
Fuente: Carro, (2009).
Tabla 1.2
Clasificación de las características.
Fuente: Carro, (2009).
1.2 La Modelización en la toma de Decisiones.
El procedimiento general para el proceso de toma de decisiones sigue los pasos bien conocidos descritos en la teoría de la gestión. Estos pasos incluyen describir el problema, recomendar una solución y monitorear el problema mediante la evaluación y actualización continua de la solución estratégica, con el fin de adaptarse a las condiciones cambiantes del negocios importante señalar que siempre existe un circuito de retroalimentación entre estos tres pasos. Cuando se identifica un problema, es fundamental analizarlo y comprenderlo antes de describirlo con precisión por escrito. Esto puede implicar el desarrollo de un modelo o marco matemático que represente con precisión la realidad, con el fin de idear posibles soluciones.
Es importante validar el modelo antes de ofrecer una solución. Este proceso requiere la capacidad de considerar múltiples perspectivas para acercarse lo más posible a la realidad. Combinando diferentes modelos desde diversas perspectivas, se puede lograr una mejor comprensión del problema. Es esencial ser específico y no abstracto en la toma de decisiones. Identificar los factores que influyen en la decisión y determinar qué está bajo control y qué no es crucial. A menos que el problema haya sido claramente formulado por el científico de la administración y aceptado como propio por quien toma las decisiones, es probable que la solución estratégica sea rechazada.
En algunos casos, la solución estratégica a un problema existente puede crear nuevos problemas, el proceso de modelado en IoT por sí solo no puede resolver los problemas de decisión; su principal objetivo es generar ideas y fomentar la creatividad para ayudar a los responsables de la toma de decisiones a tomar la decisión "correcta". El aspecto más crítico de la toma de decisiones es comprender el problema. Generalmente la formulación de un problema es más importante que su solución. De hecho, si uno puede comprender el problema, a menudo proporciona ideas sobre cómo resolverlo. En relación con la importancia de la comunicación en el modelado de IoT, se ha observado que las personas tienden a complicar las cosas innecesariamente.
Esta cuestión es particularmente destacada en los informes escritos, existe un temor común a parecer poco sofisticado o poco inteligente si uno elige escribir de manera directa y sencilla. En consecuencia, el resultado final es un producto incomprensible para quien toma las decisiones. Para superar esto, el análisis debe realizarse por etapas, con el objetivo de producir un informe que sea fácilmente comprensible para todos los lectores. Este proceso de toma de decisiones se parece mucho al enfoque estructurado que se sigue en el tratamiento de una enfermedad. Cuando un paciente se encuentra con un problema de salud, busca la ayuda de un médico para encontrar una solución. El médico, en colaboración con el paciente, describe el problema realizando pruebas o exámenes para diagnosticar la enfermedad.
Luego, el médico prescribe medicamentos y realiza visitas de seguimiento para garantizar que la acción elegida esté curando eficazmente al paciente. Si es necesario, el médico realizará cambios en la medicación. En esta analogía, el médico representa al profesional de IoT, mientras que el paciente simboliza a quien toma las decisiones y es dueño de los problemas una decisión es una elección racional hecha entre diferentes opciones es un aspecto crucial de la resolución de problemas, que cae dentro del campo más amplio de la gestión. Si bien se pueden desarrollar modelos matemáticos utilizando la ciencia de la gestión, se vuelven inútiles si la comunicación de los resultados es demasiado complicada para que la comprenda quien toma las decisiones.
La prescripción de una solución implica identificar una solución estratégica e implementarla. Se debe buscar una solución estratégica utilizando las técnicas de solución disponibles en IoT, que se discutirán más adelante. Todo problema de decisión gerencial tiene múltiples soluciones. El objetivo es lograr una solución estratégica satisfactoria, a menudo denominada "decisión correcta". No existe una solución única para los problemas del mundo real las soluciones dependen de factores como el presupuesto, el tiempo y diversas limitaciones y condiciones.
Gráfico 1.2
Descripción de la Metodología
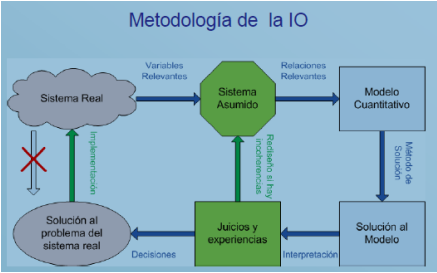
La validación del modelo es el proceso de comparar el resultado del modelo con el comportamiento del fenómeno en la realidad, implica preguntarse si el modelo que hemos construido es el adecuado para el uso previsto. La validación reconoce que ningún modelo puede capturar perfectamente todos los detalles de un sistema real y requiere determinar qué grado de desviación entre el modelo y la realidad es aceptable para el propósito previsto. La verificación del modelo, por otro lado, es el proceso de comparar el programa de computadora con el modelo para garantizar que el programa esté implementando correctamente el modelo. Hay varias razones por las que un modelo puede fallar en la validación, como la complejidad que dificulta la verificación adecuada.
En tales casos, puede ser necesario simplificar el modelo convirtiendo variables en constantes, eliminando variables, utilizando relaciones lineales en lugar de relaciones no lineales, agregando suposiciones y restricciones más estrictas o eliminando factores aleatorios. El problema de la toma de decisiones a menudo se presenta de manera distante e impersonal por parte de quien toma las decisiones, para encontrar una solución, los técnicos analizan el problema e identifican el módulo de software adecuado a utilizar. Sin embargo, es importante presentar la solución estratégica a quien toma las decisiones de una manera que pueda comprenderla, en lugar de simplemente proporcionar resultados impresos desde la computadora.
Esto requiere una interpretación gerencial de la solución, utilizando un lenguaje no técnico, a diferencia de las ecuaciones matemáticas que tienen una única solución correcta, los problemas de la vida real no tienen una respuesta definitiva. No se pueden resolver de una vez por todas, sino que requieren actualizaciones y ajustes continuos. El proceso de modelado en IO, por lo tanto, no es una ciencia exacta como las matemáticas, sino más bien un proceso en el que las decisiones deben ser tomadas en última instancia por quien toma las decisiones, las actividades de seguimiento posteriores a la prescripción desempeñan un papel crucial en el control del problema.
En un mundo en constante cambio, es necesario actualizar periódicamente las soluciones a los problemas que surgen. Incluso una solución que es válida ahora puede quedar obsoleta debido a cambios en las condiciones, convirtiéndola en una representación inexacta de la realidad. Esto puede afectar negativamente la capacidad de quien toma las decisiones para tomar las decisiones correctas, cualquier modelo utilizado debe ser capaz de adaptarse y responder a los cambios. No se debe pasar por alto la importancia de la retroalimentación y el control en el proceso de toma de decisiones, sería un error ignorar el hecho de que no existe una solución permanente para un problema de decisión empresarial. La naturaleza misma del entorno en el que se toman las decisiones es de cambio constante, lo que hace que la retroalimentación y el control sean componentes esenciales del proceso de modelado en IO.
Durante la validación, el profesional de IoT pregunta cómo se relaciona el modelo con el mundo real, los modelos que no se van a implementar ni tomar en serio desde el principio no se desarrollan correctamente. Es importante analizar y revisar cuidadosamente la información y su vigencia en el momento en que se recibe. Una vez obtenido un modelo válido, éste puede utilizarse como herramienta para la toma de decisiones, implementar el modelo no es una tarea sencilla y no debe darse por sentado, el desarrollador debe considerar cuidadosamente cómo poner el modelo en práctica y utilizarlo de forma eficaz.
Esto resalta la importancia de involucrar a quien toma las decisiones en todos los pasos del proceso de construcción del modelo, especialmente cuando el desarrollador y la persona que toma las decisiones no son la misma persona. Al incluir a quien toma las decisiones, aumentan considerablemente las posibilidades de que el modelo se implemente adecuadamente. Sin embargo, también deben tenerse en cuenta consideraciones de costes. Construir un modelo puede ser una tarea costosa. Puede que no sea prudente invertir una cantidad significativa de dinero, como 500 000 dólares, en el desarrollo de un modelo que sólo produce un rendimiento de 50 000 dólares. La razón de este alto costo radica en la
La complejidad de un modelo matemático puede aumentar con el tiempo a medida que se le incorporan más entradas y restricciones. Identificar y relacionar adecuadamente estos elementos dentro del modelo requiere una cantidad significativa de tiempo y esfuerzo, ya que debe capturar con precisión las complejidades de un sistema complejo, a medida que el modelo se vuelve más complejo, también aumenta la probabilidad de errores o interpretaciones erróneas. Esto puede dar como resultado que el modelo represente de manera inexacta la realidad o produzca resultados completamente falsos. Estas imprecisiones pueden tener graves consecuencias para la toma de decisiones y el éxito general de una empresa. Por lo tanto, es crucial garantizar la precisión al definir y expresar un problema matemáticamente, la aceptación de un modelo durante su implementación también es de gran importancia.
Si el individuo que debe utilizar el modelo no lo acepta, entonces su valor disminuye. Esta falta de aceptación puede deberse a varios factores, como una falta de comprensión del modelo o de las técnicas utilizadas para resolverlo por parte de quien toma las decisiones, o una falta de comprensión del gestor y su entorno específico por parte del desarrollador del modelo. Estos factores, incluidas las preguntas, el lenguaje y los criterios del gerente, desempeñan un papel vital a la hora de determinar qué se considera importante en el modelo. Al utilizar estas estrategias, es posible superar las limitaciones del proceso de modelado analítico y crear modelos que representen y resuelvan eficazmente problemas del mundo real. Para que los modelos contribuyan eficazmente a la toma de decisiones empresariales, es esencial comprender los beneficios y las complejidades tanto del modelo en sí como del proceso de construcción.
Para comprender plenamente la importancia de las técnicas de toma de decisiones empleadas en la organización industrial (IO), es necesaria una comprensión clara del papel del modelo y los pasos involucrados en su creación. Un aspecto clave del uso exitoso de modelos es reconocer que son abstracciones; su propósito no es proporcionar una solución definitiva a un problema de decisión, sino más bien ofrecer información valiosa que ayude en la toma de decisiones. Es importante que el modelo logre un equilibrio, evitando la replicación de todas las complejidades de la realidad, ya que esto dificultaría su resolución y proporcionaría conocimientos limitados para quien toma las decisiones, el modelo tampoco debería simplificarse demasiado hasta el punto de perder su conexión con el mundo real. Este equilibrio se aplica a todo tipo de modelos, ya sean verbales, mentales o matemáticos, ya que todos constan de variables independientes, variables dependientes, parámetros y constantes. Los modelos verbales tienen la ventaja de poder reunir estos elementos de forma natural e intuitiva, ayudando a la comprensión y la comunicación efectiva, a medida que pasamos de modelos verbales a modelos mentales y matemáticos, se hace necesario definir estos elementos con mayor precisión.
El proceso de construcción del modelo es un proceso iterativo. Desarrollar un modelo utilizable no es una tarea que pueda lograrse en un solo intento, ni siquiera para el desarrollador de modelos más experimentado. Más bien, es un proceso que implica formular y validar el modelo, seguido de posibles intentos de reformulación y revalidación. Este proceso iterativo continúa hasta que se logra un cierto nivel de confianza en la utilidad del modelo. La razón por la que diferentes gerentes toman decisiones diferentes cuando se enfrentan al mismo problema radica en el hecho de que todos somos individuos únicos con diferentes experiencias y orígenes. Las experiencias de vida de cada persona moldean su mente de una manera distinta, y el conocimiento en sí es un fenómeno biológico. Como resultado, cada ser humano percibe e interactúa con el mundo a su manera. A través de sus procesos cognitivos internos, cada individuo entabla una relación creativa con el mundo externo, contribuyendo a la amplia gama de miles de modelos diferentes.
1.4 Algunas diferencias entre el Diseño y la Materialización del Modelo.
La existencia y crecimiento de la brecha entre la teoría y la aplicación de modelos para la toma de decisiones puede atribuirse a varios factores. En primer lugar, los problemas reales suelen ser difíciles de definir y analizar, lo que dificulta la creación de modelos precisos, si bien puede ser más fácil desarrollar planes, la implementación de estos modelos a menudo se pasa por alto o no se le da la debida consideración. Esta falta de preparación desde el principio conduce a una utilización ineficaz de los modelos. Otro factor que contribuye es la falta de colaboración estrecha entre el creador del modelo y el propietario del problema. Las organizaciones a menudo no ven los beneficios directos e inmediatos de la colaboración, lo que lleva a una falta de confianza en la capacidad del modelo para resolver el problema sin causar ningún daño.
Se puede facilitar el establecimiento de confianza y el fomento de la voluntad de cooperar compartiendo experiencias de casos anteriores, la disponibilidad de datos plantea un desafío importante, ya que a menudo están dispersos, incompletos e inexactos. Para ahorrar costos y lograr resultados más rápidos, algunas empresas se conforman con resultados aproximados que se basan en datos limitados y más suposiciones. Este enfoque puede ahorrar tiempo y dinero en la recopilación de datos, pero compromete la precisión y confiabilidad de los resultados, es necesario influir en la cultura y la actitud hacia el diseño de modelos dentro de la comunidad empresarial. Esto requiere gerentes mejor capacitados y equipados para comprender y utilizar modelos analíticos de manera efectiva.
Desafortunadamente, muchas empresas invierten mucho en promociones de marketing, pero sólo asignan recursos mínimos para estudiar la eficacia de estos esfuerzos, los gerentes a menudo carecen de la capacitación adecuada en los conceptos y el uso de modelos analíticos, lo que contribuye aún más a la brecha entre la teoría y la aplicación. Es crucial que los modeladores aborden los problemas que los gerentes consideran importantes desde una perspectiva de ahorro de costos, ya que esto aumentará la probabilidad de una implementación y utilización exitosa de los modelos.
Los modelos de toma de decisiones se pueden dividir en dos categorías principales: modelos deterministas y modelos probabilísticos. En los modelos deterministas, las buenas decisiones se toman en función de sus resultados positivos, sin ningún riesgo involucrado. Los resultados de una decisión están influenciados por factores no controlables y la capacidad de quien toma la decisión para controlar estos factores a través de la información disponible. Por otro lado, los modelos probabilísticos tienen en cuenta tanto el valor del resultado como el nivel de riesgo asociado a cada decisión. Quien toma las decisiones debe determinar qué tipo de modelo es el más adecuado para el problema en cuestión. Por tanto, es importante analizar y clasificar diferentes modelos antes de proceder con el proceso de toma de decisiones. Si bien IoT se centra principalmente en modelos matemáticos, existen otros tipos de modelos que se utilizan ampliamente en la práctica. Estos modelos se pueden clasificar en función de diversas características, como su tipo, cómo evolucionan en el tiempo y la disponibilidad de información, este proceso de clasificación se ilustra en el siguiente Gráfico.
Gráfico 1.3
Modelos
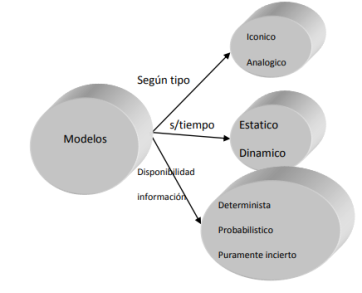
Fuente: Carro, (2009).
Los modelos mentales/verbales son traducciones de modelos mentales al lenguaje. Expresan las relaciones funcionales entre variables. Por ejemplo, un director de publicidad podría expresar su creencia de que un comercial de 20 segundos tiene más impacto en el público objetivo que uno de 15 segundos. Los modelos mentales/verbales son fáciles de entender y a menudo son el resultado de años de experiencia gerencial. Sin embargo, tienen limitaciones. Los tomadores de decisiones no pueden experimentar con ellos y no brindan información específica sobre cómo cambian los resultados o las medidas de efectividad con diferentes alternativas de decisión. Los modelos mecánicos, también conocidos como modelos físicos, se parecen a los objetos que representan, se utilizan para mostrar o probar el diseño de diversos elementos, desde nuevas construcciones hasta nuevos productos. Por ejemplo, en la industria de la aviación, se construyen y prueban modelos a escala de aviones en túneles de viento para analizar su aerodinámica.
De manera similar, los fabricantes de repuestos para automóviles pueden tener modelos a escala tridimensional de su planta para estudiar nuevos diseños de distribución y mejorar el flujo de materiales. Los modelos mecánicos ofrecen la ventaja de la experimentación y pueden ayudar a generar soluciones de diseño innovadoras. Sin embargo, su capacidad para resolver ciertos problemas, como la selección de cartera, la selección de medios para publicidad y la planificación de la producción, es limitada. En estos casos, los modelos matemáticos ejecutados en computadoras proporcionan un análisis más eficiente y completo. Los modelos analíticos son modelos matemáticos que simplifican y abstraen sistemas reales para obtener una comprensión más profunda de ciertos aspectos de la realidad.
Estos modelos se aplican principalmente a sistemas estáticos y deterministas. En comparación con los modelos mecánicos, los modelos matemáticos facilitan la experimentación ya que todas las variables, constantes y parámetros están relacionados explícitamente a través del lenguaje matemático. Los tomadores de decisiones pueden probar fácilmente los efectos de diferentes variables, estos modelos deben conectarse a problemas y dominios reales y verificarse y validarse mediante la práctica, existen varios tipos de modelos utilizados en diferentes contextos. Cada tipo tiene sus ventajas y limitaciones, y la elección del modelo depende del problema específico que se aborde. Los modelos icónicos suelen ser de naturaleza estática y física, pero a menudo no representan con precisión la realidad. Se utilizan principalmente en sistemas mecánicos. Por otro lado, las actividades empresariales son procesos dinámicos que siguen patrones matemáticos. Como resultado, pueden representarse mediante modelos simbólicos como los modelos algebraicos, numéricos y lógicos, entre estos modelos simbólicos, se utilizan ampliamente los modelos matemáticos y de simulación por computadora.
Un modelo de decisión es una representación simbólica de la realidad, con ciertas variables que representan las decisiones que se pueden tomar. Se trata de formular una representación de la realidad y determinar los aspectos relevantes. Por ejemplo, en un análisis de relevancia de un modelo real para una empresa, pueden surgir preguntas como si las ganancias son un insumo o una medida del desempeño, si el precio de un producto es una decisión o un parámetro, si la cantidad de producto a ser vendido es una variable de insumo o de producto, si la moral de los trabajadores es una medida del desempeño o un parámetro, cómo se puede medir la moral (por ejemplo, utilizando el ausentismo) y si la participación de mercado es una medida del desempeño y, de ser así, debería medirse. en unidades vendidas o ingresos. Por ejemplo, en el modelo normativo-estático-determinista con variables de decisión continuas, relaciones lineales y el objetivo de encontrar la solución óptima, la técnica de solución potencial se limitaría a la programación lineal.
El lenguaje de las matemáticas ofrece numerosas ventajas para los tomadores de decisiones. Los modelos matemáticos permiten probar fácilmente diferentes alternativas de decisión, constantes y valores de parámetros en variables dependientes. También son eficientes y concisos a la hora de representar problemas complejos, lo que los convierte en una forma rentable de analizar problemas. Por lo tanto, es importante analizar diversos modelos matemáticos y técnicas de solución que se utilizan comúnmente en la práctica. Los procedimientos de solución se pueden clasificar como de paso único o iterativos. En los procedimientos de un solo paso, los valores finales de todas las variables de decisión se determinan simultáneamente mediante un procedimiento bien definido.
Por otro lado, las técnicas de solución iterativa implican una serie de pasos para llegar a una solución final, obteniéndose soluciones parciales o completas en cada paso. La solución óptima es aquella que ha demostrado ser al menos tan buena como cualquier otra, según los supuestos del modelo, mientras que una solución satisfactoria se considera "buena" con respecto a los objetivos y restricciones, pero puede no ser la mejor. Los modelos de simulación enfrentan desafíos en su aceptación por parte de los gerentes debido a su nivel de abstracción. Los gerentes que carecen de suficiente capacitación o exposición a estos modelos, así como aquellos que están capacitados pero no tienen tiempo para brindarles la atención adecuada, pueden resistirse a su uso. Los modelos matemáticos tienen sus limitaciones debido al lenguaje simbólico de las matemáticas.
Los modelos analógicos, si bien están diseñados para imitar la realidad, pueden no parecerse mucho a ella. Los modelos complejos, como los que involucran un aeropuerto internacional, pueden requerir simplificaciones significativas para resolverse de manera eficiente, desviándose potencialmente del problema original y provocando efectos desastrosos en la organización. Por lo tanto, es necesaria una selección cuidadosa del tipo de modelo y la técnica de solución para minimizar los errores. Los modelos de simulación, por el contrario, proporcionan simulaciones por computadora de sistemas reales y son más realistas, particularmente para modelar sistemas dinámicos y/o probabilísticos como un aeropuerto internacional.
1.5 Elementos Estructurado para la toma de Decisiones.
En el proceso de modelado de toma de decisiones, analizamos el efecto de presentar diferentes decisiones retrospectivamente, como si ya se hubieran tomado de acuerdo con varios cursos de acción. Esto requiere considerar la secuencia de pasos a la inversa. Por ejemplo, primero debemos considerar el resultado, que es el resultado de nuestra acción, como si la decisión ya se hubiera tomado bajo un curso de acción diferente. Las interacciones entre estos componentes están representadas por funciones matemáticas que representan relaciones de causa y efecto entre entradas, parámetros y el resultado. También hay grupos de restricciones que se aplican a cada componente, por lo que no deben tratarse por separado, dado que el modelo de un sistema representa los elementos que impactan el objetivo de una decisión, es crucial identificar los elementos más importantes. Estos elementos suelen estar determinados por el resultado deseado, que luego determina los insumos controlables.
Las entradas de un sistema se pueden clasificar como controlables o incontrolables, es esencial seleccionar cronogramas de revisión de modelos que sean lo suficientemente cortos para que los datos incontrolables o el conocimiento probabilístico que tenemos sobre ellos no cambien significativamente. El resultado de este proceso se conoce como medida del rendimiento del sistema, cuando el resultado de una decisión depende del curso de acción, modificamos aspectos de la situación problemática para lograr un cambio deseado en otro aspecto. Esto se puede lograr comprendiendo la interacción entre los componentes del problema. Un principio general en la toma de decisiones es que si algo no se puede medir, no se puede gestionar. Por lo tanto, medir el desempeño conduce a la mejora e informar que el desempeño acelera la mejora.
El Gráfico 1.4 ilustra el proceso estructurado de toma de decisiones en el contexto de IoT. Como se muestra en el diagrama de actividades mencionado anteriormente, el proceso de toma de decisiones consta de varios componentes. La medida de desempeño proporciona el nivel deseado de resultado, que es el objetivo de la decisión, identificar el objetivo es crucial para la identificación del problema. La principal tarea del tomador de decisiones es encontrar una solución que equilibre diferentes objetivos y seleccione el que tenga el mayor valor. Si es necesario, todos los demás objetivos deben incluirse como restricciones a satisfacer. El curso de acción representa la decisión final y la estrategia óptima para lograr el objetivo deseado, tomar una decisión implica seleccionar un curso de acción para perseguir el objetivo. El impacto de un curso de acción en el resultado depende de cómo se interrelacionan los insumos y parámetros del problema y cómo se relacionan con el resultado. Los aportes incontrolables provienen del entorno de quien toma las decisiones y a menudo crean problemas y restringen las acciones. Los parámetros son elementos constantes que cambian durante el horizonte temporal de la revisión de la decisión y definen parcialmente el problema.
Gráfico 1.4
Estructuración del Proceso de Toma de Decisiones.
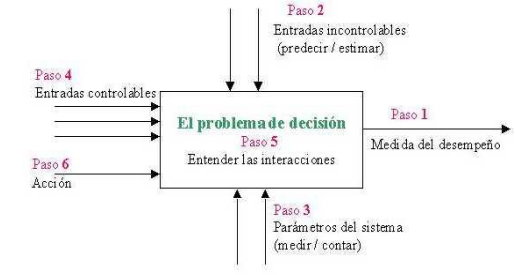
Fuente: Carro, (2009).
Durante la década de 1950, se desarrolló en el prestigioso Instituto Tecnológico de Massachusetts (MIT) una metodología de sistemas revolucionaria llamada Dinámica de Sistemas. El cerebro detrás de este enfoque innovador fue Jay W. Forrester, un consumado ingeniero electrónico que previamente había hecho importantes contribuciones al campo de las memorias magnéticas. La participación de Forrester en el desarrollo del sistema SAGE, un sistema de alerta en tiempo real de vanguardia, lo llevó a reconocer el inmenso valor de un enfoque sistémico para comprender y controlar entidades complejas que surgen de la interacción entre humanos y máquinas. Impulsado por sus experiencias, Forrester pasó a desempeñar un puesto docente en la MIT Sloan School of Management.
Fue durante este tiempo que hizo una observación fascinante: notó la aparición de fenómenos de retroalimentación dentro de las empresas, que podían provocar oscilaciones muy parecidas a los servomecanismos que había estudiado anteriormente. Esta comprensión llevó a Forrester a idear Dinámica Industrial, una metodología revolucionaria que permitió la creación de modelos cibernéticos para simular procesos industriales. Lo que distinguió a estos modelos fue su capacidad única para simular la evolución temporal de estos sistemas con la ayuda de computadoras. Posteriormente, Forrester amplió su metodología para abordar problemas de planificación urbana, dando como resultado el nacimiento de System Dynamics. El impacto de la dinámica de sistemas creció exponencialmente en la década de 1970, especialmente después de que el influyente Club de Roma encargó a Forrester y su equipo estudiar los efectos del crecimiento demográfico y la actividad humana en un mundo con recursos limitados. Forrester encabezó la creación de un modelo mundial inicial, que sirvió de base para el innovador informe conocido como "Los límites del crecimiento".
Dirigida por D.L. Meadows y financiado por la Fundación Volkswagen, este informe arroja luz sobre los problemas apremiantes que enfrentó la humanidad y las consecuencias de nuestras acciones. Además, otro informe, titulado "La humanidad en el punto de inflexión", también se basó en System Dynamics y fue encargado por Mesarovic y Pestel. Los principios subyacentes de la dinámica de sistemas tienen sus raíces en las características inherentes de los sistemas sociales y las limitaciones de los propios seres humanos. Según Forrester, los sistemas como empresas, organizaciones, mercados y economías son cerrados y no lineales en su estructura. Se consideran cerrados porque las decisiones tomadas por los individuos dentro de estos sistemas tienen un efecto dominó que influye en las decisiones posteriores. Por ejemplo, si un director de marketing decide lanzar una campaña de marketing, el resultado de esa campaña afectará posteriormente a los procesos de toma de decisiones futuros.
Cuando una empresa promociona uno de sus productos, puede crear dificultades para otros productos dentro de la misma empresa. Esto puede dar lugar a comportamientos indeseables, como oscilaciones, especialmente si los efectos de la promoción se manifiestan con retraso. Por otro lado, hay efectos de refuerzo que ocurren cuando una empresa es la primera en ingresar a un nuevo mercado y obtiene una ventaja competitiva a través de la innovación y relaciones sólidas con los clientes. Estos circuitos de retroalimentación desempeñan un papel crucial en la configuración del sistema general, dentro de un mismo sistema, puede haber múltiples bucles de retroalimentación operando a diferentes velocidades, dependiendo del tiempo que tarda una causa en producir un efecto, las conexiones entre las variables de un sistema suelen ser no lineales, lo que significa que los efectos se multiplican en lugar de simplemente sumarse.
El comportamiento de un sistema, incluida la participación de mercado, la ventaja comparativa y las relaciones con los competidores, está determinado por sus entidades estructurales y las relaciones causales entre ellas. Este comportamiento puede ser muy complejo y dinámico, incluso en estructuras aparentemente simples. Ejemplos de comportamientos tan complejos incluyen el crecimiento en forma de S, el crecimiento exponencial, la reacción exagerada, el crecimiento y el colapso, y la oscilación, todos los cuales pueden analizarse examinando la estructura subyacente.
1.6 Las limitaciones de la Naturaleza Humana.
Recientemente se ha puesto énfasis en el pensamiento sistémico, que puede verse como un lenguaje utilizado para abordar eficazmente las complejidades e interdependencias que los administradores encuentran a diario. Frente a estos sistemas complejos, los individuos se esfuerzan por comprender su comportamiento para poder dar una explicación válida. Sin embargo, nuestras capacidades cognitivas son principalmente adecuadas para un mundo estable que carece de cambios rápidos, donde principalmente consideramos sólo lo que está cerca en el tiempo y el espacio. En consecuencia, a menudo cometemos errores de juicio al descuidar la relevancia de variables y conexiones que están distantes en el tiempo o remotas en el espacio. Esta perspectiva limitada conduce a modelos mentales y a una toma de decisiones incompleta que produce efectos secundarios inesperados e incluso molestos.
1.7 Diagramas Causales o de Lazos.
Un diagrama de bucle causal comprende cuatro elementos esenciales: variables, vínculos entre ellas, signos de los vínculos (que demuestran interconexiones) y signos del bucle (que indican el comportamiento del sistema). Al adoptar una perspectiva sistémica, se pueden analizar los problemas para identificar las fuerzas subyacentes que impulsan el comportamiento observado, los diagramas causales juegan un papel crucial en el estudio de sistemas dinámicos de dos maneras. En primer lugar, durante la fase de desarrollo del modelo, sirven como esbozo inicial de la hipótesis causal. En segundo lugar, ayudan a simplificar la ilustración del modelo. En ambos casos, estos diagramas permiten a los analistas comunicar de manera efectiva la comprensión estructural del sistema según el modelo. Ampliando el trabajo realizado por Forrester, el concepto de diagramas causales se utiliza ampliamente en el modelado de sistemas.
Estos diagramas, que se dibujan utilizando diversos programas informáticos, permiten la simulación y predicción de los resultados del modelo con una variación mínima en su representación. El proceso de construcción de vínculos causales implica varios pasos. En primer lugar, las variables se crean y nombran en consecuencia. A continuación, se dibujan enlaces para establecer conexiones. Luego se nombra el bucle y, finalmente, se recorre para comprender sus implicaciones. Los diagramas de vínculos causales pueden verse como oraciones construidas identificando variables clave e indicando sus relaciones causales a través de vínculos. Estos vínculos están representados por flechas, que se originan en variables independientes y terminan en variables dependientes. Al interconectar estos vínculos, se puede crear una narrativa coherente para abordar temas o problemas específicos. Para ilustrar más estos conceptos, consideremos un ejemplo tomado de Study Notes in System Dynamics de Michael R. Goodman, cap. 1. Los sistemas dinámicos se basan en las interacciones de bucles de retroalimentación, y los diagramas de flujo y los diagramas causales sirven como representaciones visuales de estas estructuras cíclicas antes de su posterior desarrollo en redes consistentes con tasas, niveles y elementos auxiliares.
Al diagramar bucles causales, los modeladores pueden obtener una comprensión conceptual de los sistemas del mundo real en términos de bucles de retroalimentación.
1.8 Modelo Migración Población, Migración, Empleo.
Diagrama 1.1
Diagrama Causal
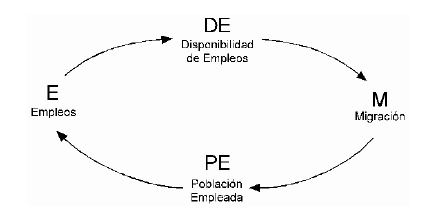
La relación entre la migración y la disponibilidad de empleos en DE es compleja e involucra varios ciclos de retroalimentación. La disponibilidad de empleos en DE atrae inmigrantes a la ciudad, lo que a su vez aumenta la población de empleados. Este crecimiento demográfico conduce a la absorción de empleos disponibles, pero también crea una demanda de más servicios urbanos y, en última instancia, resulta en la expansión de empleos tanto E como DE. El aumento del número de puestos de trabajo disponibles en la ciudad también tiene un impacto en la disponibilidad de puestos de trabajo DE. A medida que se crean más puestos de trabajo, también aumenta la disponibilidad de puestos de trabajo en DE. Esto significa que cuantas más oportunidades laborales haya en la ciudad, más opciones habrá para las personas que buscan empleo en el sector DE.
La migración y la disponibilidad de empleos DE están interconectadas en un sistema donde una afecta a la otra. Esta relación puede explicarse a través de una serie de hipótesis causales que resaltan los circuitos de retroalimentación involucrados en el funcionamiento urbano. En el largo plazo, la población ocupada en la ciudad demanda más servicios urbanos. Esto se debe a que a medida que hay más personas empleadas, necesitan acceso a diversos servicios como transporte, atención médica y educación. El aumento de la demanda de estos servicios conduce a la expansión del número total de empleos E disponibles en la ciudad. Con más gente en la fuerza laboral, los empleos disponibles en la ciudad comienzan a ser absorbidos. Esto significa que a medida que la población crece, el número de oportunidades laborales disminuye porque están siendo ocupadas por los recién llegados. A medida que estos inmigrantes llegan, contribuyen al crecimiento de la población de empleados en la ciudad. Este aumento de población es el resultado de que los recién llegados se unen a la fuerza laboral y se suman al número total de empleados en la ciudad. La primera hipótesis afirma que la disponibilidad de empleos en DE conduce a una afluencia de inmigrantes hacia la ciudad, esto significa que cuando hay oportunidades laborales en la ciudad, es más probable que la gente migre allí en busca de empleo. El proceso de creación de este diagrama paso a paso proporcionará una explicación detallada de cómo representar ciclos o bucles de manera efectiva. Para diagramar con precisión la estructura de un ciclo y determinar su polaridad, es necesario establecer conexiones entre todos los pares de variables pertinentes.
1.9 Relaciones Causa-Efecto Modelos de Aplicación.
Las variables en este contexto son las siguientes: Empleos (E), que se refiere al número total de vacantes y puestos de trabajo cubiertos en el área urbana; Disponibilidad de Empleo (DE), que representa el número de puestos de trabajo vacantes; Migración (M), que significa la migración de la población trabajadora al área urbana; y Población Ocupada (PE), que indica la población ocupada residente en la zona.
Otro ejemplo de relación positiva involucra las variables Migración (M) y Población Ocupada (PE). Representamos esta relación de la misma manera que la relación DE-M anterior. El Diagrama 1.2 ilustra la relación M-PE, donde un aumento en la tasa de migración (M) conduce a un aumento en el número de personas empleadas, expandiendo así la población residente empleada. La flecha sirve como indicador de la dirección de la influencia, mientras que el signo más (+) o menos (-) indica el tipo de influencia. Cuando hay un aumento en la Disponibilidad de Empleo (DE), se produce un aumento en la Migración (M). Por lo tanto, la relación entre las dos variables se indica con un signo "+", que indica una correlación positiva. Para aplicar esta definición, solo consideramos pares de variables adyacentes entre sí. De manera similar, podemos usar esta definición con ligeros ajustes para determinar la polaridad de circuitos cerrados de retroalimentación. En un sentido más amplio, si todas las demás variables permanecen constantes, un cambio en una variable da como resultado un cambio en la misma dirección para la segunda variable, en comparación con su valor anterior. Esto se conoce como una relación positiva entre las variables.
Diagrama 1.2
Disponibilidad de Empleos Positivo Lazo Migración
Una relación negativa se indica con un signo "-" y se caracteriza por la ocurrencia de un cambio en una variable que resulta en un cambio en la dirección opuesta en la segunda variable. Esta relación negativa se representa visualmente en el diagrama 1.3
Diagrama 1.3
Población Empleada Positivo. Lazo Migración
Diagrama 1.4
Disponibilidad de Empleos Negativo. Lazo Población Empleada-
Vale la pena señalar que cuando dos pares de relaciones negativas se conectan, en realidad crean una relación positiva a lo largo de toda la cadena. En este caso, las variables A, B y C están encadenadas negativamente, como se muestra en el Diagrama. Cuando la variable A aumenta, provoca una disminución en B, lo que a su vez conduce a un aumento en la variable C. Como resultado, se considera que la cadena de A a C tiene una relación positiva. Los diagramas 1.3 y 1.4 presentan un supuesto causal sobre la relación entre la población residente ocupada y la disponibilidad de empleos en un área urbana. Según la Figura 4, un aumento en el número de residentes empleados eventualmente conducirá a una disminución en la disponibilidad de empleo. Esto se debe a que a medida que nuevos trabajadores ingresan a la ciudad, llenan los puestos de trabajo disponibles, reduciendo así el número total de oportunidades laborales. Por el contrario, si la población de trabajadores residentes comienza a disminuir, se puede suponer que habrá más puestos de trabajo disponibles. Por lo tanto, cualquier aumento o disminución de la población ocupada dará como resultado el cambio opuesto en la disponibilidad de empleo.
Diagrama 1.5
Los Causales.
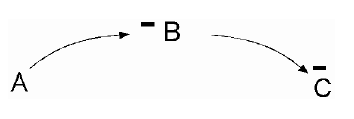
Diagrama 1.6
Lazo Causal Simple.
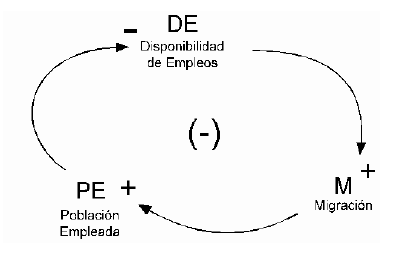
Los diagramas 1.5 y 1.6 muestra un circuito de retroalimentación negativa, indicado por el signo "-" en el centro del ciclo ilustran las relaciones interconectadas entre los pares DE, M y PE. Para determinar la polaridad del ciclo completo, debemos considerar las consecuencias de un cambio hipotético en la variable del ciclo. El aumento de la disponibilidad laboral se ve reforzado por la cadena positiva entre PE y E. Para determinar la polaridad del nuevo ciclo, podemos examinar el efecto de un aumento significativo en la disponibilidad laboral dentro de ese ciclo, ignorando todas las demás cadenas fuera de él. Este aumento resultaría en una migración hacia el área urbana, lo que llevaría a un aumento de la Población Ocupada. Esto, a su vez, eventualmente aumentaría el número de empleos básicos, mejorando así la disponibilidad de empleo. Consideremos un escenario en el que hay un aumento repentino en la disponibilidad de empleo. Este aumento de ED atraería a más personas a la ciudad, lo que resultaría en un aumento de la Población Ocupada (PE). Entonces, la DE aumenta la PE, un aumento de la Población Ocupada conduce a una disminución de la Disponibilidad de Empleo.
Las causas internas que inicialmente aumentaron la DE han desencadenado una serie de reacciones y ajustes internos dentro del sistema. Estos cambios crean presiones que se oponen a cualquier cambio adicional en DE. Por lo tanto, el ciclo tiende a mantener un valor u objetivo fijo para la DE, a pesar de que las influencias externas empujan en la dirección opuesta. Cuando un sistema consta de múltiples ciclos, es necesario determinar la polaridad de cada ciclo de forma aislada. Esto implica suponer que todas las demás variables fuera del ciclo (y dentro de él) permanecen constantes. Cada ciclo tendrá su propia polaridad. Para determinar la polaridad de un ciclo, el método sugerido es comenzar desde un punto del sistema con una suposición, como por ejemplo asumir que hay crecimiento en ese punto.
Luego, recorre todo el ciclo y observa el efecto al regresar, si el efecto va en aumento, el ciclo es positivo; si no, es negativo, si el efecto recibido es del mismo signo, el ciclo es positivo; si es de signo contrario, el ciclo es negativo. Cuando un circuito de retroalimentación responde a un cambio en una variable en dirección opuesta a la perturbación original, lo llamamos ciclo negativo. Por otro lado, cuando el ciclo responde reforzando la perturbación original, se le denomina ciclo positivo, los diagramas 1.6 presenta una cadena positiva entre la Población Ocupada (PE) y el Empleo (E). Esta cadena supone que un aumento de la Población Ocupada eventualmente conducirá a un aumento de los Empleos, debido al aumento de la demanda de diversos servicios como vivienda, construcción, etc. El modelo ahora consta de dos ciclos cerrados: el conocido ciclo negativo compuesto por DE , M y PE; y un nuevo ciclo positivo (externo) que involucra las cuatro variables, la introducción de esta nueva cadena no afecta la polaridad del ciclo compuesto por DE, M y PE.
Diagrama 1.7
Dos Ciclos.
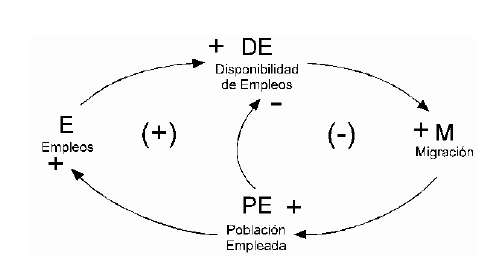
1.10 Modelo de la Oferta con retardo.
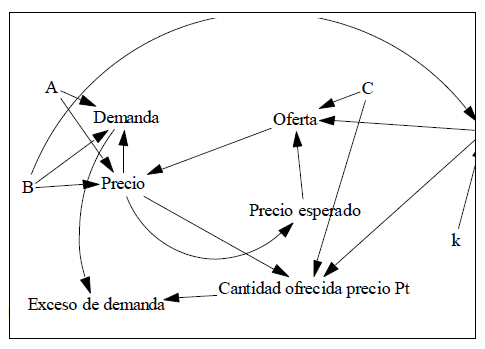
Este modelo particular se puede aplicar a mercados donde el proceso de producción es largo y el producto no se puede almacenar. En este modelo, asumimos que la cantidad demandada del producto en un momento dado es una función lineal de su precio, expresado como Demanda = A - B * Precio. Por otro lado, la cantidad ofrecida por los productores depende del precio que inicialmente esperaban recibir por el producto, representado como Oferta = C + E * Precio esperado. Es importante señalar que en este escenario el producto no es almacenable, por lo que los productores aceptarán el precio máximo que los consumidores estén dispuestos a pagar para agotar su producción, incluso si difiere de sus expectativas iniciales, los productores forman sus expectativas de precios basándose en el precio de mercado del período anterior, adoptando un enfoque más ingenuo.
Es necesario analizar la tendencia de los precios en un lapso de 100 años en las tres situaciones. Esto implica examinar diferentes períodos de tiempo y comparar la cantidad demandada por los consumidores con la cantidad que los productores habrían ofrecido si hubieran tenido conocimiento del precio vigente en el momento de tomar la decisión de producción.
CAPÍTULO II
EL PROCESO DE TOMA DE DECISIONES ANTE SITUACIONES QUE IMPLICAN RIESGO E INCERTIDUMBRE.
2. EL RIESGO.
Para ilustrar la distinción entre modelos probabilísticos y deterministas, consideremos el pasado y el futuro, si bien no podemos alterar el pasado, cualquier acción que emprendamos en el presente tiene el potencial de influir y dar forma al futuro, aunque sea incierto. Los directivos suelen priorizar la configuración del futuro en lugar de insistir en acontecimientos pasados. Los sistemas pueden permanecer sin cambios o sufrir cambios con el tiempo aquellos que permanecen estáticos se conocen como sistemas deterministas, mientras que la mayoría de las organizaciones que encontramos son sistemas dinámicos que evolucionan constantemente, cuando un sistema sigue un patrón típico de desarrollo, nos referimos a él como si tuviera un patrón de comportamiento.
Que un sistema sea estático o dinámico depende del marco temporal de estudio elegido y de las variables en las que se centra, el horizonte temporal se refiere al período específico en el que se analiza el sistema, mientras que las variables son los valores cambiantes dentro del sistema. Anteriormente, analizamos cómo los sistemas se componen de varias partes que trabajan juntas para lograr un objetivo específico. Las relaciones entre estas partes son cruciales para determinar la funcionalidad y el funcionamiento generales del sistema. De hecho, estas relaciones suelen tener más importancia que las propias partes individuales. Cuando los sistemas se construyen utilizando sistemas más pequeños, se les denomina subsistemas. La probabilidad juega un papel importante en el proceso de toma de decisiones, ya que ayuda a navegar situaciones con información limitada y un alto grado de incertidumbre de hecho, es raro tener acceso a todos los datos necesarios a la hora de tomar decisiones, la probabilidad es un concepto crucial que los gerentes deben considerar cuando se enfrentan a la incertidumbre.
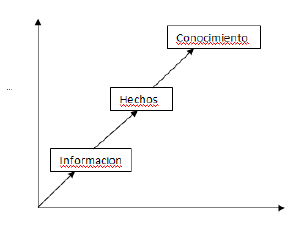
El conocimiento es la acumulación de lo que entendemos y comprendemos. Es la base sobre la que construimos nuestra comprensión del mundo. La información, por otro lado, es el medio a través del cual se comunica y comparte el conocimiento, es la transferencia de conocimiento de una entidad a otra. Los datos, a menudo denominados información bruta, no se consideran conocimiento en sí mismos, es la etapa inicial en el proceso de transformación hacia el conocimiento, el viaje de los datos al conocimiento implica varios pasos. Primero, los datos se convierten en información cuando se vuelven relevantes y útiles en el contexto de la toma de decisiones. Luego, esta información se refina y verifica aún más y, en última instancia, se convierte en hechos cuando está respaldada por evidencia y datos concretos. La información se puede clasificar en dos formas distintas: explícita y tácita. La información explícita está estructurada y puede explicarse y comprenderse fácilmente. Puede transmitirse a través de instrucciones, directrices o manuales claros. Por el contrario, la información tácita es más difícil de articular, ya que a menudo se basa en experiencias personales, intuición o emociones. Es subjetivo y no fácilmente transferible, lo que hace que su explicación sea inconsistente e imprecisa. En resumen, conocimiento e información son conceptos estrechamente entrelazados. El conocimiento es lo que sabemos y entendemos, mientras que la información es el medio a través del cual se comunica el conocimiento. La transformación de datos en conocimiento implica varias etapas, incluida la conversión de datos en información y de información en hechos.
El conocimiento no es estático sino dinámico, influenciado por incertidumbres y expresado con cierto grado de confianza, en última instancia, el conocimiento se vuelve valioso cuando se utiliza de manera efectiva en los procesos de toma de decisiones, lo que conduce a mejores resultados y avances. En cualquier intercambio de conocimiento intervienen dos partes: el emisor y el receptor. El remitente es responsable de hacer accesible a otros su conocimiento privado transformándolo en información. Esta comunicación de información puede adoptar diversas formas, como comunicación verbal o escrita, representaciones visuales o incluso señales no verbales.
El conocimiento realmente evoluciona hacia su forma completa cuando se aplica con éxito en los procesos de toma de decisiones, es a través de la utilización de hechos e información que el conocimiento se convierte en una herramienta poderosa que ayuda a completar con éxito diversas tareas y desafíos, es importante señalar que el conocimiento no se basa únicamente en hechos. El conocimiento instrumental, que es conocimiento práctico utilizado en los procesos de toma de decisiones, a menudo se expresa con cierto grado de confianza estadística. Esto significa que el conocimiento no es absoluto ni definitivo sino que está influenciado por diversos factores e incertidumbres.
En un entorno incierto, la probabilidad de tomar "buenas decisiones" aumenta cuando se tiene acceso a "buena información". El grado de estructuración en el proceso de Gestión del Conocimiento contribuye a la disponibilidad de información tan valiosa, el diagrama refuerza la noción de que a medida que mejora la precisión de un modelo estadístico, la toma de decisiones también experimenta un aumento correspondiente en efectividad. El diagrama anterior muestra la correlación entre la precisión de un modelo estadístico y el nivel de mejora en la toma de decisiones. Destaca el papel crucial de las estadísticas empresariales en nuestra sociedad, la estadística surgió de la necesidad de establecer una base sistemática para el conocimiento, lo que implicaba estudiar leyes de probabilidad, medir propiedades y analizar relaciones de datos.
Gráfico 2.1
Exactitud del Modelo Estadístico.
Niveles de mejoras en la toma de Decisiones.
2.1. De los datos a un conocimiento decisivo.
La probabilidad juega un papel crucial en tales situaciones, actuando como sustituto de la certeza y el conocimiento completo. Los modelos probabilísticos se basan en aplicaciones estadísticas que ayudan a evaluar eventos o factores incontrolables y evaluar los riesgos asociados con la toma de decisiones. Originalmente, el campo de la estadística tenía como objetivo recabar información para el Estado. Curiosamente, el término "estadística" no tiene raíces griegas o latinas, sino que proviene de la palabra italiana para estado. Por otra parte, la probabilidad tiene una historia mucho más larga. Sus raíces se remontan al verbo "probar", que implica el acto de descubrir información que no se obtiene ni se comprende fácilmente.
De hecho, la palabra "prueba" comparte el mismo origen, proporcionando los detalles necesarios para comprender lo que se considera verdadero. Los modelos probabilísticos pueden compararse con un juego, en el que la toma de decisiones se guía por resultados anticipados. Este cambio de un enfoque determinista a uno probabilístico implica el empleo de métodos estadísticos subjetivos para la estimación, prueba y predicción. Dentro de estos modelos, el concepto de riesgo se refiere a la presencia de incertidumbre, cuya distribución de probabilidad está bien definida. En consecuencia, realizar una evaluación de riesgos implica un examen de los resultados potenciales de las decisiones, junto con sus probabilidades asociadas.
Un ejemplo de sabiduría en acción es la creación de software estadístico que no sólo sea técnicamente avanzado sino que también tenga un propósito práctico. Se ha observado que la llegada de Internet y su amplia popularidad nos proporciona grandes cantidades de información, pero no nos brinda la sabiduría para comprender y utilizar esa información de manera efectiva.
Este paso implica limpiar y preparar los datos para el análisis, identificar cualquier valor atípico o error y seleccionar métodos estadísticos apropiados para analizar los datos. Las técnicas de análisis estadístico pueden variar según la naturaleza de los datos y los objetivos del proceso de toma de decisiones. Las técnicas estadísticas comunes incluyen estadística descriptiva, estadística inferencial, análisis de regresión y prueba de hipótesis. El proceso de toma de decisiones estadísticas se refiere a un enfoque sistemático utilizado por individuos u organizaciones para tomar decisiones informadas basadas en análisis estadístico e interpretación de datos. Este proceso implica varios pasos que están diseñados para garantizar que las decisiones se tomen de manera lógica y objetiva, teniendo en cuenta varios factores y minimizando el potencial de sesgos o errores. Una vez analizados los datos, el siguiente paso es interpretar los resultados.
Esto implica sacar conclusiones de los datos y comprender las implicaciones de los hallazgos. Es importante considerar las limitaciones e incertidumbres asociadas con los datos y el análisis, así como cualquier posible sesgo o factor de confusión que pueda haber influido en los resultados. Finalmente, una vez que se ha tomado una decisión, es importante monitorear y evaluar los resultados. Esto implica evaluar la efectividad de la decisión y determinar si es necesario realizar algún ajuste o modificación. Al monitorear y evaluar los resultados, las personas u organizaciones pueden aprender de sus decisiones y mejorar su proceso de toma de decisiones en el futuro, una vez definido el problema, entonces es necesario iniciar la captación de los datos requeridos.
En este sentido, se recopila información y datos de diversas fuentes, que pueden incluir encuestas, experimentos, observaciones o bases de datos existentes. Los datos recopilados deben ser relevantes y representativos del problema en cuestión, asegurando que proporcionen una comprensión integral y precisa de la situación. El primer paso en el proceso de toma de decisiones estadísticas es definir claramente el problema u objetivo en cuestión. Esto implica identificar la decisión específica que se debe tomar y comprender el contexto y los antecedentes de la situación. Al definir claramente el problema, los individuos u organizaciones pueden centrar sus esfuerzos en recopilar los datos relevantes y realizar el análisis necesario, el proceso de toma de decisiones estadísticas es un enfoque sistemático y lógico que se utiliza para tomar decisiones informadas basadas en el análisis estadístico y la interpretación de datos.
Al seguir este proceso, las personas u organizaciones pueden garantizar que las decisiones se tomen de manera racional y objetiva, lo que conducirá a resultados más efectivos y exitosos. Con base en la interpretación de los resultados, el siguiente paso es tomar una decisión. Esto implica sopesar la evidencia y considerar las implicaciones de diferentes opciones o cursos de acción. Es importante considerar los riesgos y beneficios potenciales de cada opción, así como cualquier consideración ética o legal.
2.2 Toma de Decisiones Estadística.
A diferencia de los procesos deterministas de toma de decisiones como la optimización lineal, que implican resolver un conjunto de ecuaciones, los sistemas paramétricos de ecuaciones y la toma de decisiones bajo pura incertidumbre implican una mayor cantidad de variables que son más difíciles de cuantificar y verificar, esta complejidad se ve contrarrestada por el hecho de que es más fácil de comprender que un evento observado, lo que hace que su resolución sea más manejable y eficiente en términos de tiempo, el modelo se puede aplicar a problemas similares varias veces y también se puede adaptar y modificar según sea necesario. En comparación, la gama de métodos probabilísticos y estadísticos disponibles para analizar la toma de decisiones en condiciones de incertidumbre se ha ampliado significativamente y se ha vuelto más eficaz.
Los tomadores de decisiones a menudo encuentran importantes lagunas de información. La evaluación de riesgos sirve para cuantificar la diferencia entre lo que se sabe y lo que se requiere para tomar una decisión óptima. Los modelos probabilísticos sirven como salvaguardias contra la incertidumbre adversa y la explotación de dicha incertidumbre. El origen de la teoría de la decisión para la toma de decisiones surge del concepto de función de utilidad de pago. Este propone que las decisiones se deben tomar calculando la utilidad y probabilidad de varias opciones dentro de un rango, estableciendo estrategias para una toma de decisiones efectiva. Fundamentalmente, la toma de decisiones implica combinar información sobre probabilidades con deseos e intereses. Este enfoque, que trata las decisiones como si fueran apuestas, sirve como base de la teoría de la decisión. Requiere sopesar el valor de un determinado resultado frente a su probabilidad de ocurrencia. En el ámbito de los modelos probabilísticos, a menudo se los compara con juegos, donde las acciones se basan en resultados anticipados.
El cambio de modelos deterministas a probabilísticos implica la utilización de técnicas estadísticas subjetivas para la estimación, prueba y predicción. Dentro de estos modelos, el riesgo se refiere a la incertidumbre con una distribución de probabilidad conocida. Por lo tanto, la evaluación de riesgos implica un estudio integral que determina los resultados potenciales de las decisiones junto con sus respectivas probabilidades. Cuando entra en el proceso, asume el papel de sustituto de la certeza, llenando los vacíos del conocimiento completo. Los modelos probabilísticos se basan en aplicaciones estadísticas que evalúan eventos y factores incontrolables, así como también evalúan los riesgos asociados con la toma de decisiones. Inicialmente, las estadísticas tenían como objetivo recopilar información para el Estado, y el término en sí proviene de la palabra italiana "bienestar". Por otro lado, la probabilidad tiene una historia más larga, derivada del verbo "probar", que denota la búsqueda de comprensión y obtención de conocimiento. La palabra “prueba” comparte el mismo origen, aportando los detalles necesarios para comprender lo que se considera verdadero.
Los desafíos de la toma de decisiones se ejemplifican aún más por la complejidad de las alternativas disponibles. Quienes toman decisiones deben lidiar con información limitada al considerar las implicaciones de un solo curso de acción, en muchos casos, también deben prever y comparar las implicaciones de múltiples cursos de acción. Además, a menudo entran en juego factores desconocidos y el resultado rara vez es seguro. A menudo, el resultado depende de las reacciones de otros individuos que tal vez ni siquiera sean conscientes de sus propias acciones. En consecuencia, no es sorprendente que a veces los tomadores de decisiones retrasen sus decisiones el mayor tiempo posible o tomen decisiones sin considerar plenamente todas las implicaciones.
Cuando las personas se enfrentan a la toma de decisiones, a menudo optan por seleccionar una opción sin considerar detenidamente todas las posibles consecuencias que pueden surgir. Tomar decisiones implica el proceso de integrar información relacionada con las probabilidades con los propios deseos e intereses. Un aspecto clave de la teoría de la decisión es abordar las decisiones como si fueran apuestas, en las que los individuos deben equilibrar el valor de un resultado particular con su probabilidad de que realmente suceda. El concepto de teoría de la decisión se originó a partir del concepto de función de utilidad de pago, que sugiere que las decisiones deben tomarse evaluando la utilidad y la probabilidad asociadas con varias alternativas, al emplear estrategias que priorizan la toma de decisiones efectiva, las personas pueden navegar las complejidades de la elección y optimizar sus resultados.
Diagrama 1.1
Estrategias para la toma de Decisiones.
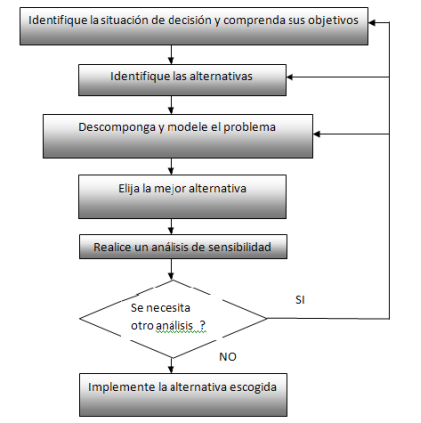
Este capítulo proporciona una visión general integral del proceso de análisis de alternativas para la toma de decisiones. Explora el uso de diferentes criterios de decisión, varios tipos de información e información de diferente calidad. El capítulo profundiza en los elementos implicados en el análisis de decisiones y alternativas de elección, incluidas las metas y objetivos que guían la toma de decisiones, también examina las preferencias de alternativas en la toma de decisiones, junto con los criterios y métodos de elección. Además, el capítulo presenta herramientas de evaluación de riesgos. Los objetivos juegan un papel crucial en este proceso ya que ayudan a identificar problemas y evaluar soluciones alternativas. Al evaluar alternativas, es esencial que quien toma las decisiones exprese sus objetivos como criterios que reflejen con precisión los atributos de las alternativas relevantes para la elección.
2.3 Proceso de Toma de Decisiones.
Los objetivos del análisis de decisiones son incorporar orientación, información, discernimiento y estructura al proceso de toma de decisiones para mejorar su racionalidad y eficacia. A diferencia de los procesos deterministas de toma de decisiones, como la optimización lineal resuelta mediante ecuaciones, las decisiones que implican incertidumbre suelen tener una mayor cantidad de variables que son más difíciles de medir y controlar, los pasos para resolver estas decisiones siguen siendo los mismos. En primer lugar, es necesaria la simplificación para dividir el problema en componentes manejables. Luego, se construye un modelo de decisión para representar la situación real de manera simplificada. El modelo no necesita capturar cada detalle o relación, sino que se centra en los aspectos fundamentales ignorando los factores irrelevantes.
Esto permite una resolución de problemas más sencilla con un mínimo esfuerzo e inversión de tiempo, el modelo se puede utilizar repetidamente para problemas similares y se puede ajustar según sea necesario, los seres humanos son capaces de comprender, comparar y manipular números. Por lo tanto, al crear un modelo de análisis de decisiones, es crucial establecer la estructura del modelo y asignar probabilidades y valores. Esto incluye determinar probabilidades, funciones de valor para evaluar alternativas, ponderaciones de valor para medir compensaciones entre objetivos y preferencias de riesgo. El análisis de decisiones es una disciplina que implica evaluar alternativas complejas considerando tanto los valores (a menudo en términos monetarios) como la incertidumbre. Proporciona información sobre las diferencias entre las alternativas definidas y genera sugerencias para mejores alternativas.
Los números se utilizan para cuantificar valores subjetivos e incertidumbres, lo que permite una mejor comprensión de la situación de decisión. Sin embargo, estos resultados numéricos deben traducirse en información cualitativa para uso práctico. Una vez que se definen la estructura y los números, se puede comenzar el análisis. El análisis de decisiones implica algo más que simplemente calcular la utilidad esperada y ponderada de cada alternativa. También requiere examinar la sensibilidad de estas empresas de servicios públicos a las probabilidades clave y a los parámetros de ponderación de riesgo, la realización de análisis de sensibilidad permite calcular el valor de la información perfecta para incertidumbres modeladas explícitamente. Afortunadamente, ahora existen métodos probabilísticos y estadísticos más numerosos y potentes disponibles para analizar la toma de decisiones en condiciones de incertidumbre.
Los avances en la tecnología informática han hecho que estas aplicaciones prácticas sean más accesibles. Algunos ejemplos de aplicaciones comerciales incluyen auditores que utilizan técnicas de muestreo aleatorio para auditar cuentas por cobrar, gerentes de planta que utilizan técnicas estadísticas de control de calidad para garantizar la calidad del producto, analistas financieros que utilizan métodos de regresión y correlación para comprender los indicadores financieros, analistas de marketing que emplean pruebas de significancia para evaluar compradores potenciales, y gerentes de ventas que utilizan técnicas estadísticas para predecir las ventas.
2.4 Modelos de Decisión Estocásticos.
Una de las formas más sencillas de formular un problema de decisión es empleando una Matriz de Beneficios, también conocida como Matriz de Pagos. Esta matriz proporciona una representación clara de los posibles beneficios financieros asociados con cada alternativa de decisión. Más adelante profundizaremos en este concepto. El análisis de decisiones es un proceso sistemático que permite a quien toma las decisiones seleccionar una sola decisión entre una variedad de alternativas posibles, particularmente cuando hay incertidumbre sobre el futuro. El objetivo final es optimizar el resultado en términos de un criterio de decisión numérico específico, como maximizar el pago o el retorno, también hay un número finito de alternativas de decisión disponibles para quien toma las decisiones.
Estas alternativas de decisión, denominadas miembros del conjunto A, representan las acciones potenciales que se pueden adoptar. Sin embargo, quien toma las decisiones sólo puede elegir una alternativa. Por tanto, una decisión exitosa requiere explorar una gama diversa de alternativas más allá de las opciones iniciales o de las tradicionalmente aceptadas. Es crucial ser conciso en los aspectos lógicos y racionales del proceso de toma de decisiones. Si bien puede haber innumerables características o factores a considerar, no todos son esenciales para tomar decisiones. Con frecuencia es suficiente tener un puñado de alternativas.
El objetivo principal de esta investigación es observar y analizar el comportamiento de quien toma decisiones cuando se enfrenta a una elección entre diferentes cursos de acción, donde los resultados están influenciados por el azar o las acciones de los competidores. Los componentes clave de los problemas de análisis de decisiones incluyen la presencia de una persona que tiene la responsabilidad de tomar la decisión, como un director ejecutivo que debe rendir cuentas ante los accionistas, existe un número finito de posibles eventos futuros denominados estados de la naturaleza, que abarcan una variedad de escenarios posibles. Estas circunstancias, en las que se toman decisiones, se conocen como estados de naturaleza y se categorizan y organizan dentro del conjunto S. Cada estado de naturaleza es mutuamente excluyente, lo que significa que sólo uno puede ocurrir a la vez. Surge la pregunta: ¿qué puede hacer la naturaleza? En el ámbito de la toma de decisiones, pueden surgir diversas fuentes de errores. Los supuestos falsos, la falta de estimaciones precisas de las probabilidades, la dependencia excesiva de las expectativas, las dificultades para medir la función de utilidad y los errores de juicio son factores que pueden contribuir a errores en la toma de decisiones en situaciones de riesgo.
Diagrama 1.2
Elementos de un Modelo Probabilístico.
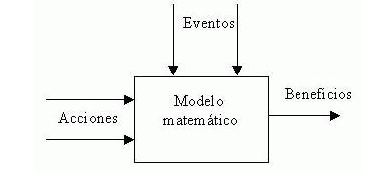
Se analiza la siguiente decisión de inversión.
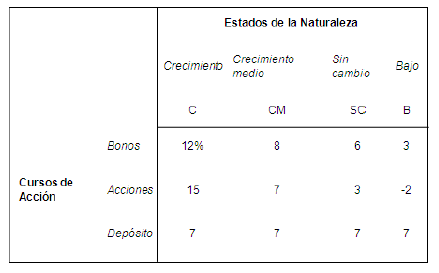
Los estados de naturaleza hacen referencia a las diferentes condiciones económicas que pueden darse a lo largo de un año. El desafío es determinar el mejor curso de acción entre las tres opciones disponibles, cada una de las cuales ofrece diferentes tasas de rendimiento, como se indica en la tabla 2.1.
Los modelos de análisis de decisiones se pueden aplicar en varios escenarios y su dominio abarca un espectro que se extiende entre dos situaciones contrastantes. El grado en que poseemos información sobre los resultados de nuestras acciones determina exactamente en qué lugar de este espectro cae un determinado modelo de análisis de decisiones.
Tabla 2.1
Modelo de Incertidumbre.
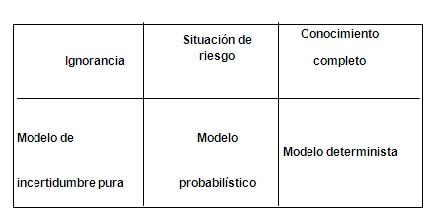
Las situaciones de decisión caracterizadas por una incertidumbre plana plantean el mayor nivel de riesgo, para simplificar esta idea, consideremos un escenario con sólo dos resultados posibles. Este concepto se alinea con la noción de Bayes de que la evaluación de la probabilidad es siempre subjetiva. En otras palabras, la probabilidad asignada a un evento depende del conocimiento y la información disponibles para quien toma la decisión. Si quien toma las decisiones posee toda la información relevante, la probabilidad pasa a ser 1 o 0. La probabilidad sirve como herramienta para medir la probabilidad de que ocurra un evento. Cuando usamos probabilidad, esencialmente estamos expresando el nivel de incertidumbre.
En el lado determinista, donde el resultado es seguro, la probabilidad es 1 o 0. Por el contrario, el otro extremo de la escala representa una probabilidad plana, donde todos los resultados son igualmente probables. Por ejemplo, si estamos completamente seguros acerca de la ocurrencia o no ocurrencia de un evento, asignamos una probabilidad de uno o cero, respectivamente, cuando surge la incertidumbre y no estamos seguros del resultado, utilizamos la expresión "realmente no lo sé", indicando un 50% de probabilidad de que suceda o no, la escala que estamos discutiendo aquí abarca dos extremos: el determinismo y la incertidumbre pura, en la primera parte ya hemos explorado los problemas asociados con el determinismo, en el otro extremo de la escala se encuentra la pura incertidumbre, donde no se puede predecir el resultado de un evento, entre estos dos extremos, encontramos problemas que entran dentro de la categoría de riesgo.
Existen diferentes tipos de modelos de decisión que se pueden utilizar para analizar diferentes escenarios en función de la cantidad y el grado de conocimiento disponible. Los tres tipos más utilizados son: decisiones tomadas con pura incertidumbre, decisiones tomadas con riesgo y decisiones tomadas comprando información para reducir la incertidumbre. Es importante señalar que las decisiones tomadas con pura incertidumbre suelen ser más adecuadas para la toma de decisiones personales que para la toma de decisiones públicas. Las figuras públicas, como los gerentes, deben tener algún conocimiento sobre los posibles resultados para poder predecir sus probabilidades y tomar decisiones informadas. Cuando quien toma las decisiones tiene algún conocimiento sobre los resultados, puede asignar probabilidades subjetivas a cada resultado, lo que clasifica el problema como toma de decisiones bajo riesgo. Por ejemplo, al tomar una decisión de inversión, es posible que quien tome la decisión deba considerar el estado de la economía durante el año siguiente.
Pueden limitar las posibilidades de crecimiento, igualdad o decadencia, y buscar la opinión de especialistas para determinar las probabilidades de cada estado, esta información adicional puede ayudar a tomar una mejor decisión, en algunos casos, quien toma las decisiones puede buscar la experiencia de especialistas para reducir sus incertidumbres sobre las probabilidades de cada resultado, esto se puede hacer comprando información relevante a especialistas, lo que se conoce como enfoque de Bayes. Al incorporar el asesoramiento de expertos a sus incertidumbres, quien toma las decisiones puede tomar una decisión más informada y razonable, para tomar decisiones informadas, es necesaria información relevante para reducir la incertidumbre, la evaluación de la probabilidad es simplemente una forma de cuantificar la incertidumbre y comunicarla entre individuos.
Permite comunicar la incertidumbre en relación con eventos, estados del mundo, creencias y más, la probabilidad sirve como herramienta para transmitir incertidumbre. El resultado de un evento se puede predecir con una cierta probabilidad, denotada como p. La variación en los resultados posibles es p(1-p), y esta variación es mayor cuando p es igual al 50%, lo que significa que hay la misma probabilidad para cada resultado. En tal caso, la calidad de la información está en su nivel más bajo, ya que la variación en los datos es alta. Es importante señalar que la calidad de la información y la variación están inversamente relacionadas, lo que significa que una mayor variación en los datos conduce a una disminución en la calidad de la información. Las decisiones tomadas con pura incertidumbre ocurren cuando quien toma las decisiones no tiene conocimiento sobre la probabilidad de algún resultado. En estas situaciones, el comportamiento de quien toma las decisiones se basa únicamente en su actitud hacia lo desconocido. Esto puede manifestarse como optimismo, pesimismo, arrepentimiento u otros comportamientos.
Gráfico 2.3
La Relevancia de la Información disminuye la Incertidumbre.
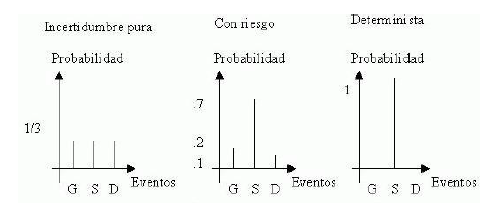
2.6 Tomar Decisiones en la Incertidumbre
La toma de decisiones en condiciones de pura incertidumbre está influenciada por los rasgos de personalidad de quien toma las decisiones una actitud pesimista o conservadora lleva a centrarse en minimizar las pérdidas y seleccionar alternativas que ofrezcan la mayor protección contra resultados negativos, esta mentalidad está impulsada por la creencia de que los eventos desfavorables son más probables y requiere la asignación de probabilidades que se alineen con esta perspectiva. Cuando las decisiones se toman en un estado de incertidumbre, quien toma las decisiones carece de conocimiento sobre los resultados de los diferentes escenarios posibles o la adquisición de dicha información es costosa. En tales situaciones, la decisión está influenciada predominantemente por los rasgos de personalidad de quien toma la decisión.
Para abordar esta incertidumbre, quien toma las decisiones debe asignar probabilidades a diferentes resultados, transformando el problema de uno de incertidumbre a uno de riesgo. En primer lugar, tenemos la actitud pesimista o conservadora, a menudo denominada enfoque Maximin. Este enfoque se basa en la creencia de que los acontecimientos desafortunados le suceden constantemente a quien toma las decisiones. En consecuencia, la toma de decisiones en este contexto implica adoptar la mentalidad de minimizar las pérdidas potenciales y seleccionar alternativas que proporcionen el más alto nivel de protección contra resultados negativos. Este enfoque cauteloso está impulsado por una creencia profundamente arraigada de que es probable que se materialice el peor de los casos.
Quien toma decisiones que emplea una actitud pesimista o conservadora tiende a asignar probabilidades de una manera que refleja su creencia en el peor de los casos. Asignan
mayores probabilidades a resultados desfavorables, operando bajo el supuesto de que los eventos más perjudiciales tienen más probabilidades de ocurrir. Este enfoque permite a quien toma decisiones prepararse y mitigar pérdidas potenciales, incluso ante la incertidumbre. En este escenario, la mentalidad de quien toma las decisiones está moldeada por una visión del mundo pesimista, donde la atención se centra en protegerse de daños potenciales en lugar de correr riesgos. Quien toma las decisiones tiende a priorizar la evitación de resultados indeseables, incluso si eso significa sacrificar ganancias potenciales. Esta actitud conservadora está impulsada por el miedo a lo desconocido y la falta de confianza en los resultados positivos.
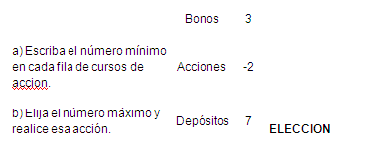
Mantengo una actitud optimista y asertiva, adoptando el enfoque maximax, que se puede resumir en la creencia de que constantemente obtengo resultados favorables
El coeficiente de optimismo, también conocido como coeficiente de Hurwicz, permite a las personas lograr un equilibrio entre el optimismo excesivo y el pesimismo extremo. Este coeficiente se representa en una escala de 0 a 1, donde 1 indica una perspectiva muy optimista y 0 simboliza una perspectiva profundamente pesimista. Al seleccionar un valor entre estos dos extremos, los individuos pueden adoptar un enfoque intermedio que no anticipe excesivamente resultados positivos ni espere excesivamente resultados negativos. Este enfoque equilibrado promueve una mentalidad más realista y práctica.
A modo de ilustración, cuando α es igual a 0,7, podemos aplicar estos pasos.
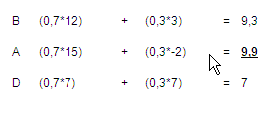
Matriz de Arrepentimiento.
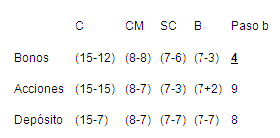
Al tomar decisiones en condiciones de pura incertidumbre, quien toma las decisiones carece de conocimiento o información sobre qué resultado potencial o "estado de naturaleza" es más probable que ocurra. Esta falta de conocimiento a menudo lleva a que quien toma las decisiones no pueda adoptar una postura pesimista u optimista. En estos casos, quien toma las decisiones se centra en garantizar la seguridad y minimizar los riesgos potenciales. En el campo del análisis de decisiones, generalmente se supone que quien toma las decisiones se enfrenta a un problema en el que debe seleccionar una opción, y sólo una, de un grupo de opciones potenciales, en determinadas situaciones, estas limitaciones pueden superarse abordando la toma de decisiones en condiciones de incertidumbre como un juego de suma cero entre dos personas.
Es importante señalar que cualquier técnica o método utilizado en la toma de decisiones en condiciones de pura incertidumbre sólo es adecuado para decisiones personales en la vida privada de un individuo. Por el contrario, una figura pública como un gerente debe poseer cierta comprensión o conciencia de los estados potenciales de la naturaleza para poder predecir con precisión las probabilidades asociadas con cada resultado. Sin este conocimiento, quien toma las decisiones sería incapaz de justificar o defender sus elecciones de manera lógica y razonable.
La calidad de la estrategia óptima depende en última instancia de la precisión de su evaluación. Los tomadores de decisiones deben examinar e identificar cuidadosamente la sensibilidad de la estrategia óptima en relación con los factores clave involucrados. Esto permite una comprensión más completa de los posibles resultados y consecuencias asociados con cada alternativa, una gestión de riesgos eficaz requiere una evaluación y un análisis cuidadosos de los posibles resultados y consecuencias. Quienes toman decisiones deben evaluar estrategias alternativas y asignar probabilidades a factores inciertos. Al seguir un proceso sistemático de toma de decisiones, los gerentes pueden tomar decisiones bien informadas que minimicen los riesgos y maximicen los resultados positivos. En situaciones en las que quienes toman las decisiones poseen algún conocimiento sobre los estados potenciales de la naturaleza, pueden asignar probabilidades subjetivas a la probabilidad de que ocurra cada estado. Este tipo de toma de decisiones se denomina toma de decisiones arriesgadas, ya que implica asignar probabilidades a la ocurrencia de diferentes estados de la naturaleza.
El proceso de toma de decisiones implica varios pasos. En primer lugar, se define cuidadosamente el problema en cuestión y se consideran detenidamente todas las alternativas viables. Luego, cada alternativa se evalúa en función de los resultados potenciales que puede producir. Esta evaluación se puede realizar examinando la recuperación monetaria, la ganancia neta en activos o los aspectos relacionados con el tiempo de cada alternativa, los factores inciertos se cuantifican en términos de su probabilidad. El riesgo implica un nivel de incertidumbre y la capacidad de tener control total sobre los resultados o consecuencias de ciertas acciones. Gestionar y eliminar riesgos es una responsabilidad crucial de los directivos. Sin embargo, es importante reconocer que la eliminación de un riesgo puede conducir potencialmente a la aparición de otros riesgos. Para garantizar una gestión de riesgos eficaz, es necesario evaluar y analizar el impacto potencial de las decisiones tomadas durante el proceso de gestión de riesgos. Esto permite a los tomadores de decisiones evaluar estrategias alternativas antes de llegar a una decisión final.
El Criterio de Laplace reconoce la falta de conocimiento sobre los estados de la naturaleza y trata todas las posibilidades como igualmente probables. Al asignar probabilidades iguales y considerar los resultados ponderados, quienes toman decisiones pueden tomar decisiones mejor informadas a pesar de la incertidumbre que rodea la situación. El Criterio de Laplace, también conocido como "No sé nada", se basa en el supuesto de que todos los estados de la naturaleza tienen la misma probabilidad de ocurrir. Este criterio se utiliza cuando existe falta de conocimiento o información sobre los diferentes resultados posibles.
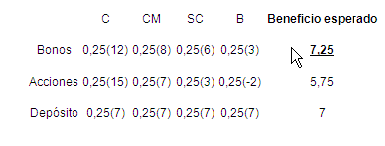
Para ampliar la declaración dada, podemos introducir múltiples filas de cursos de acción y proporcionar ejemplos de beneficios esperados asociados con cada opción. Este paso es crucial en los procesos de toma de decisiones, especialmente cuando se utilizan matrices y árboles de decisión, que se explicarán y explorarán con más detalle en el capítulo 14 de este libro. Una vez que se han identificado todas las opciones y sus respectivos beneficios esperados, es importante seleccionar el curso de acción que ofrezca la mayor ganancia potencial según lo determinado en el paso c. Siguiendo este método, los individuos pueden tomar decisiones informadas de manera efectiva utilizando matrices y árboles de decisión, que se discutirán en detalle más adelante en el libro.
2.7 Consideración de los Riesgos.
En nuestras discusiones anteriores, nos centramos en tablas de distribución que se basaban en el valor monetario esperado como criterio para la toma de decisiones, es importante reconocer que el valor del dinero puede variar en diferentes situaciones y según diferentes decisiones. No se trata de una relación lineal sencilla en la que más dinero siempre equivale a más valor. Esto significa que, como analistas, debemos considerar la utilidad monetaria de quien toma las decisiones y seleccionar cursos de acción que proporcionen la utilidad esperada más alta, en lugar de simplemente centrarnos en el valor monetario esperado más alto. Hay dos razones importantes por las que los beneficios monetarios esperados no siempre son razonables como criterio para la toma de decisiones. En primer lugar, es posible que el valor monetario no refleje verdaderamente el valor personal que un resultado particular tiene para un individuo.
Esto es evidente en situaciones en las que la gente está dispuesta a jugar a la lotería por cantidades de dinero relativamente pequeñas. En segundo lugar, aceptar los valores monetarios esperados como único criterio puede no reflejar con precisión la aversión al riesgo de un individuo. Para ilustrar esto, consideremos un escenario en el que a uno se le ofrecen 10 dólares por no hacer nada o la oportunidad de participar en una apuesta que depende del lanzamiento de una moneda, con una recompensa potencial de 1.000 dólares por cara y una pérdida de 950 dólares por cruz. La primera opción tiene una recompensa esperada de $10, mientras que la segunda tiene una recompensa esperada mayor, la decisión de elegir cualquiera de las opciones dependerá de la aversión al riesgo de un individuo, y aceptar por sí solo los valores monetarios esperados pueden no reflejar con precisión esta preferencia, las actitudes de las personas hacia el riesgo y sus diferencias individuales influirán en gran medida en su proceso de toma de decisiones. Si bien las personas pueden enfrentar situaciones similares, no necesariamente toman las mismas decisiones debido a sus diferentes percepciones del riesgo.
Es importante señalar que esto no significa que todos deban correr el mismo riesgo en situaciones similares, incluso si dos personas tienen criterios similares y enfrentan la misma situación, sus reacciones pueden diferir según su estabilidad financiera personal, las diferencias personales en opinión e interpretación de las políticas también pueden contribuir a divergencias en las decisiones. Cuando se trata de pagos de seguros individuales, el objetivo principal es evitar posibles pérdidas financieras asociadas con eventos no deseados, la utilidad de estos resultados no puede ser directamente proporcional a sus consecuencias monetarias. Si la pérdida potencial se percibe como significativa, es más probable que las personas estén dispuestas a pagar una prima más alta por la cobertura del seguro, si la pérdida se considera intrascendente, es posible que las personas no estén motivadas a pagar por ella.
La pregunta fundamental entonces es: ¿Cómo medimos la función de utilidad para cada tomador de decisiones? La decisión de contratar o no un seguro varía entre diferentes personas e implica un complejo proceso de toma de decisiones influenciado por factores psicológicos y económicos, entre otros. Un aspecto crucial en este proceso es el concepto de utilidad, que apunta a medir el beneficio percibido que el dinero tiene para quien toma decisiones individuales. Al emplear el concepto de utilidad, podemos entender por qué algunas personas están dispuestas a gastar 1 dólar en billetes de lotería con la esperanza de ganar un millón de dólares. Por lo tanto, para tomar una decisión acertada que tenga en cuenta la actitud de quien toma la decisión hacia el riesgo, es necesario transformar la matriz de beneficios monetarios en una matriz de utilidad. Al definir una matriz de utilidad de esta manera, podemos comprender mejor las preferencias y los patrones de toma de decisiones de los individuos cuando se enfrentan a resultados inciertos.
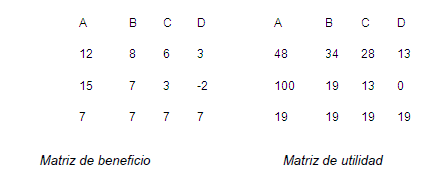
Todos los métodos mencionados anteriormente ahora se pueden utilizar en esta matriz de utilidad, que se centra en factores no monetarios, para llegar a una decisión satisfactoria. Cabe señalar que la decisión puede variar según estos enfoques.
2.8 Respuestas con respecto al riesgo y su impacto.
La teoría de la decisión no proporciona una descripción clara de cómo las personas realmente toman decisiones, ya que existen desafíos para calcular probabilidades y determinar la utilidad de los resultados. La racionalidad subjetiva de las personas y la percepción del problema de decisión también pueden influir en su proceso de toma de decisiones, gestionar eficazmente el riesgo requiere considerar la probabilidad de que ocurra un evento y el impacto que tiene. Quienes toman decisiones deben tener en cuenta factores tanto cuantitativos como cualitativos, entendiendo que el valor esperado por sí solo puede no capturar con precisión el verdadero nivel de riesgo. Al evaluar la complejidad de estos factores, quienes toman decisiones pueden tomar decisiones más informadas cuando se enfrentan a la incertidumbre. La probabilidad de que ocurra un evento y el impacto que tiene son factores importantes para considerar al gestionar el riesgo y la incertidumbre. Para controlar, limitar y mitigar eficazmente el riesgo, los tomadores de decisiones deben analizar los aspectos cuantitativos y cualitativos de la gestión de riesgos. Ambos escenarios resultan en la misma pérdida esperada de $25, esto no refleja con exactitud el hecho de que el escenario 2 pueda percibirse como más riesgoso que el primero. Quien toma las decisiones puede estar más preocupado por minimizar el impacto de un evento raro pero extremo que centrarse en el resultado promedio. Esta perspectiva subjetiva pone de relieve la complejidad que implica evaluar la probabilidad de un evento, el impacto que tiene y el nivel de riesgo asociado.
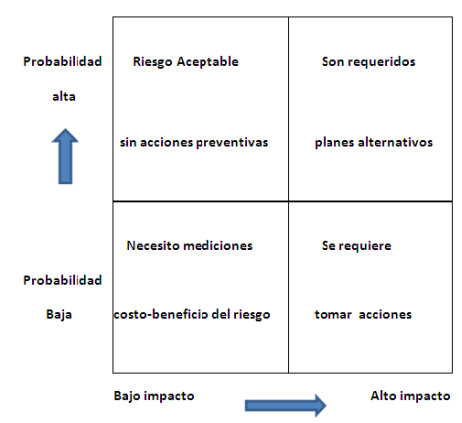
Como se mencionó anteriormente, es importante señalar que el concepto de certeza está directamente relacionado con la rentabilidad libre de riesgo, la distinción entre el nivel de certeza que posee quien toma decisiones y el valor monetario esperado (EMV) se denomina prima de riesgo. Es fundamental analizar el signo y la magnitud de la prima de riesgo para clasificar la postura del decisor frente al riesgo. Si la prima de riesgo es positiva, indica voluntad de aceptar el riesgo. Vale la pena señalar que los individuos varían en su aceptación del riesgo, y aquellos que poseen una prima de riesgo más alta están más inclinados a asumir riesgos. Por otro lado, si la prima de riesgo es negativa, quien toma las decisiones evitará activamente asumir riesgos, por lo que se le denomina aversión al riesgo. En los casos en que la prima de riesgo es cero, quien toma las decisiones se considera neutral al riesgo.
2.9 Cuando se Evalúa el Riesgo,
El riesgo es el posible inconveniente o inconveniente asociado con correr un riesgo o hacer una apuesta, y normalmente se expresa en términos de probabilidad. El control de riesgos, por otro lado, implica un proceso sistemático de evaluación de las ganancias o pérdidas potenciales asociadas con una acción o decisión específica y de asignarles valores de probabilidad apropiados. Básicamente, el control de riesgos implica la creación de una representación matemática, conocida como variable aleatoria, que representa con precisión el nivel de riesgo involucrado, el indicador de riesgo es una medida o cantidad numérica que captura y transmite eficazmente la calidad o solidez general de una decisión, teniendo en cuenta los riesgos asociados.
Analizando el problema de la Decisión de la Inversión.
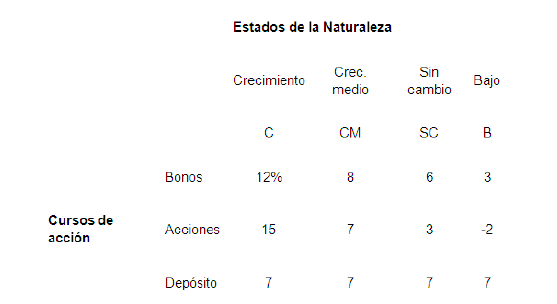
Los estados de la naturaleza se refieren a diferentes condiciones económicas que pueden ocurrir en el transcurso de un año, estas condiciones pueden variar en términos de su impacto en la economía en general. El valor esperado, también conocido como valor promedio, es una medida utilizada para estimar el resultado probable de estos diferentes estados de la naturaleza.
Ahora surge la pregunta de cómo tomar una decisión entre un curso de acción con un resultado esperado más alto y otro con un resultado esperado más bajo pero con un riesgo significativamente mayor. En tales casos, se puede emplear otra medida de riesgo llamada coeficiente de variación (CV). El CV representa el riesgo relativo en relación con el valor esperado. Se calcula dividiendo la desviación estándar por el valor esperado y multiplicando por 100%. Es importante destacar que el CV es independiente de la unidad de medida del valor esperado. También se puede utilizar la inversa del CV, conocida como relación señal-ruido. El coeficiente de variación permite representar el riesgo como porcentaje del valor esperado. La varianza es una medida de riesgo y una varianza más alta indica un riesgo mayor.
La varianza no se expresa en las mismas unidades que el valor esperado, lo que dificulta su comprensión. Para abordar este problema, se utiliza la raíz cuadrada de la varianza, conocida como desviación estándar. Tanto la varianza como la desviación estándar proporcionan la misma información y pueden derivarse entre sí. Dado que la desviación estándar es la raíz cuadrada de la varianza, se expresa en las mismas unidades que el valor esperado. La indicación de calidad para una decisión no es suficiente por sí sola. Es fundamental considerar la variación para tomar la decisión correcta. En nuestro ejemplo numérico, también nos interesa evaluar el "riesgo" comparativo asociado con diferentes cursos de acción. Una forma de medir el riesgo es mediante el uso de la desviación estándar. Tanto la varianza como la desviación estándar son valores numéricos que indican la variabilidad inherente a una decisión. Un valor de riesgo más bajo sugiere una mayor probabilidad de lograr el resultado esperado. Por tanto, el riesgo puede utilizarse para comparar diferentes cursos de acción. El resultado deseado es tener un mayor rendimiento esperado con un menor riesgo, razón por la cual al administrador le preocupa el alto riesgo.
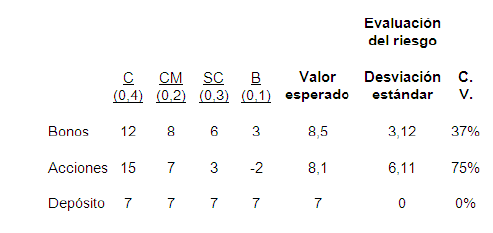
Con base en la información proporcionada en las columnas de Evaluación de riesgos de la tabla, se puede concluir con confianza que los Bonos presentan un riesgo significativamente menor en comparación con las Acciones, es evidente que los depósitos están totalmente libres de riesgos, a pesar de tener este conocimiento, la pregunta sigue siendo: ¿Cuál debería ser el curso de acción adecuado considerando toda la información relevante? A la luz de esta perspectiva, resulta aún más crucial evaluar cuidadosamente las opciones disponibles y considerar diversos factores como los objetivos financieros personales, la tolerancia al riesgo y las tendencias del mercado. Al analizar minuciosamente estos elementos, podrá tomar una decisión informada sobre el curso de acción más adecuado que se alinee con sus circunstancias y objetivos individuales. En última instancia, esta decisión está en sus manos, ya que usted es quien debe sopesar los riesgos y recompensas potenciales asociados con cada opción de inversión. En otras palabras, dado que existe una falta de conocimiento específico sobre el futuro, todos los resultados potenciales tienen la misma probabilidad.
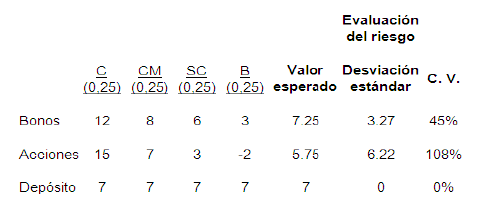
2.10 Análisis de Dos Inversiones.
Por ejemplo, considere dos alternativas de inversión: inversión uno e inversión dos. Sus características se resumen en la siguiente tabla
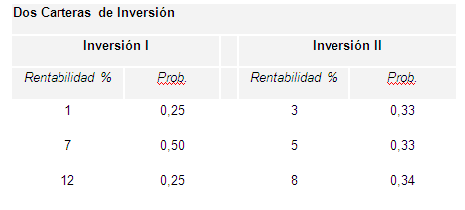
Es importante tener en cuenta que estas dos inversiones no se pueden clasificar según el análisis de media-varianza habitual. Esto se debe a que la inversión I tiene tanto el rendimiento promedio como la desviación estándar más altos. Por lo tanto, el Enfoque Estándar de Dominación no es aplicable en este caso. En lugar de ello, necesitamos reordenar el coeficiente de variación (CV) para establecer una base sistemática de comparación. Para clasificar estas dos inversiones es necesario realizar una serie de cálculos y analizar los resultados. Comencemos calculando el promedio y la desviación estándar de cada inversión.
Al hacer los cálculos, encontramos que la inversión I tiene un rendimiento promedio de 6,75% y una desviación estándar de 3,9%, mientras que la inversión II tiene un rendimiento promedio de 5,36% y una desviación estándar de 2,06%. Para ilustrar la aplicación de este análisis, consideremos una inversión de $10 000 durante un período de 4 años. Al final de cada año, la inversión rinde T(t), siendo el rendimiento de cada año estadísticamente independiente. El coeficiente de variación (CV) para la inversión I se calcula en 57,74%, mientras que para la inversión II es 38,43%. Según el CV, se prefiere la inversión II a la otra, este enfoque se puede aplicar para clasificar cualquier número de alternativas de inversión.
2.11 El Árbol de Decisiones y la Matriz.
Tenemos las consecuencias o resultados, denotados como xij, que son los resultados que ocurren cuando quien toma las decisiones selecciona una alternativa particular en respuesta a un estado específico. A continuación, tenemos las acciones o alternativas disponibles para quien toma las decisiones. Estos se representan como a1, a2, ..., am. Quien toma las decisiones debe elegir una de estas alternativas en respuesta al estado dado. En aras de la simplicidad, suponemos que existe un número finito de estados y alternativas. Esto nos permite estructurar el proceso de toma de decisiones de forma clara y organizada. En primer lugar tenemos los distintos estados posibles que puede presentar la naturaleza, denotados como F1, F2, ..., Fn. Estos estados representan los diferentes resultados o escenarios potenciales que pueden surgir.
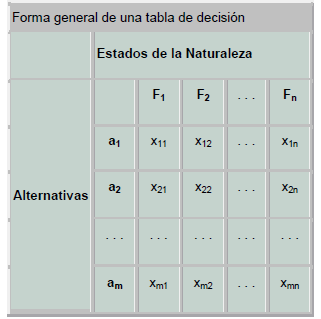
Regla de Decisión:
Dentro del entorno de incertidumbre, se pueden aplicar varias reglas de decisión, algunos de ellos incluyen el criterio de Wald, que se centra en minimizar la máxima pérdida posible; el criterio Maximax, que tiene como objetivo maximizar la máxima ganancia posible; el criterio de Hurwicz, que busca un equilibrio entre los mejores y peores resultados basándose en un coeficiente de optimismo; el criterio Savage, que minimiza el máximo arrepentimiento; y el criterio de Laplace, que considera todos los estados de la naturaleza como igualmente probables. Si bien los criterios antes mencionados se utilizan comúnmente en procesos de decisión en condiciones de incertidumbre, es importante señalar que existen muchas otras reglas de decisión válidas que pueden emplearse.
Por tanto, se hace necesario determinar las propiedades que hacen que un criterio sea preferible a otro en este contexto incierto. La tabla de decisiones sirve como una herramienta valiosa en cualquier proceso de toma de decisiones, ya que ayuda a responder la pregunta fundamental de determinar la mejor alternativa. Para realizar esta determinación, nos basamos en reglas o criterios de decisión, que pueden definirse como los valores numéricos asociados a cada alternativa en función de un criterio específico. Estos criterios de decisión se describen basándose en el conocimiento que tiene quien toma las decisiones sobre el estado de la naturaleza y la clasificación de los procesos de decisión.
Hay tres tipos distintos de tablas de decisión según el entorno en el que operan: certeza, incertidumbre y riesgo. En los procesos de decisión bajo incertidumbre, quien toma la decisión es consciente de los posibles estados de la naturaleza pero carece de información sobre cuál ocurrirá, no hay forma de cuantificar esta incertidumbre ni de predecir el estado real que surgirá. Esto significa que quien toma las decisiones no posee ninguna información probabilística sobre las posibilidades de que ocurra cada estado. Pasando a los procesos de decisión en un entorno de riesgo, se caracterizan por la capacidad de asociar una probabilidad de ocurrencia a cada estado de la naturaleza, esto significa que quien toma las decisiones tiene cierto conocimiento de la probabilidad de cada resultado.
Para ayudar en su proceso de toma de decisiones, la cadena hotelera ha recopilado información sobre el precio del terreno, la ganancia estimada que generaría el hotel si el aeropuerto estuviera ubicado en cada ubicación respectiva y el valor de venta potencial del terreno si el aeropuerto finalmente no se construye allí. Estos datos se resumen en la siguiente tabla. Imagine una ciudad que está planeando construir un aeropuerto y tiene dos ubicaciones posibles para elegir, denominadas A y B. La decisión sobre qué ubicación elegir se tomará el próximo año. En este escenario, una cadena hotelera está interesada en abrir un hotel cerca del nuevo aeropuerto. Sin embargo, deben decidir qué terreno comprar para esta empresa, las tablas de decisión en un entorno de riesgo se basan en varios criterios de decisión.
Para ilustrar estos criterios, examinamos un escenario de aplicación específico que involucra la elección de una ubicación para un nuevo aeropuerto y la decisión de una cadena hotelera sobre qué terreno comprar. Al considerar factores como el precio, la ganancia estimada y el valor de venta potencial, la cadena hotelera puede tomar la decisión más adecuada para su negocio. Ahora, ante toda esta información, la cadena hotelera necesita determinar la decisión más adecuada. En otras palabras, necesitan analizar los diversos factores en juego, como el valor esperado, la varianza, la media, la dispersión y la probabilidad, para tomar una decisión informada sobre qué terreno comprar. Al tomar decisiones en un entorno de riesgo, las tablas de decisiones suelen utilizar ciertos criterios para evaluar opciones. Estos criterios incluyen el criterio del valor esperado, el criterio de varianza mínima con media limitada, el criterio de media con varianza limitada, el criterio de dispersión y el criterio de máxima verosimilitud. Para comprender mejor cómo se aplican estos criterios, consideremos un escenario de aplicación.
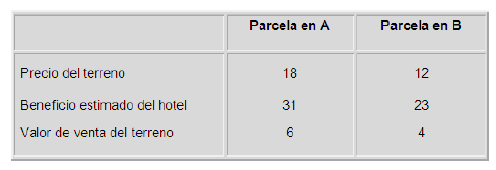
Por el contrario, si el aeropuerto se construye en B, sería necesario vender el terreno adquirido en A. En este caso, se obtendría una ganancia de 6 por la venta del terreno, pero esto se compensaría con la inversión inicial de 18. Por lo tanto, el rendimiento final en este escenario sería -12. Si la cadena hotelera decide comprar el terreno en A y finalmente se construye el aeropuerto allí, obtendrán una ganancia de 31 por la operación del hotel. Sin embargo, este beneficio se verá reducido por la inversión inicial de 18 realizada en la compra del terreno. Por lo tanto, el rendimiento final en este escenario sería 13. Estos cálculos se pueden aplicar a las alternativas restantes y a los resultados posibles, lo que da como resultado la siguiente tabla de decisiones.
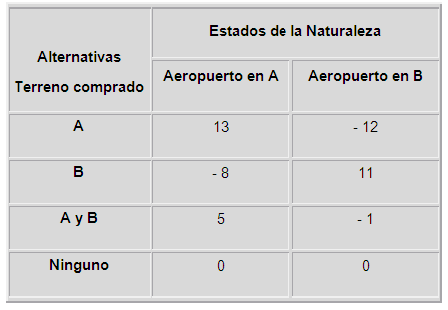
2.12 Valor Esperado.
Imagine un minorista que necesita tomar una decisión sobre la cantidad de unidades a comprar para una determinada mercancía. Dado que esta mercancía es perecedera y no puede almacenarse por más de un día, no es recomendable exceder el suministro para un día. El minorista incurre en un costo de $1 por unidad al comprarlo y lo vende por $5. Por cada unidad que se demanda pero no se compra para la venta, el minorista renuncia a una ganancia potencial de 4 dólares, sin mencionar la posible pérdida de clientes. Si el minorista tuviera un conocimiento perfecto de la cantidad exacta demandada, le resultaría obvio solicitar exactamente esa cantidad sin excederla, en realidad, nuestro minorista carece de esta información y busca orientación sobre cuánto stock mantener.
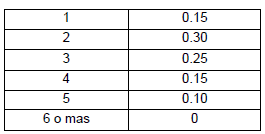
Mediante el uso de estas fórmulas podemos evaluar el beneficio de cada interacción entre los escenarios de demanda potencial y las alternativas de compra disponibles. Para crear una matriz de resultados integral, representaremos los resultados en función del beneficio que obtiene el comerciante de cada interacción entre los posibles escenarios de demanda y las alternativas de compra disponibles. Con base en la información proporcionada, se puede observar que el comerciante nunca solicitará más de 5 unidades. Por tanto, las únicas opciones de compra disponibles para el comerciante son comprar 0, 1, 2, 3, 4 o 5 unidades, los posibles resultados están determinados por la demanda, que puede ser 0, 1, 2, 3, 4 o 5 unidades.
Matriz de resultados.
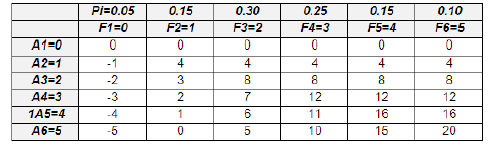
Si tuviéramos que calcular la expectativa matemática utilizando el criterio del valor esperado de los resultados, necesitaríamos elegir la solución que arroje el valor más alto, ya que es la óptima en este escenario debido a nuestra matriz de ganancias.
La decisión, en este caso, es tener un stock de 4 unidades, lo que se traducirá en una mayor ganancia esperada. Al analizar la matriz de resultados anterior, se evidencia que para cada posible escenario futuro (Fi), existe una acción alternativa (Ai) que arroja la máxima ganancia. Por ejemplo, A3 es la acción óptima para F3, A5 para F5, etc. Para cuantificar el costo de oportunidad asociado con cada resultado, calculamos la diferencia entre la ganancia máxima de Fi y el valor real del resultado. En otras palabras, el costo de oportunidad representa la ganancia potencial que pierde quien toma las decisiones al no seleccionar la acción óptima. En el caso de las matrices de costos, el costo de oportunidad refleja la cantidad de ahorros que pierde quien toma las decisiones al no elegir la acción óptima. En el ejemplo actual, desviarse de la cantidad de demanda genera un costo debido a no seleccionar la mejor estrategia alineada con el valor de la demanda. Cuando la cantidad de existencias coincide con el valor de la demanda, el costo de oportunidad es cero porque representa la ganancia máxima alcanzable para ese valor de demanda en particular.
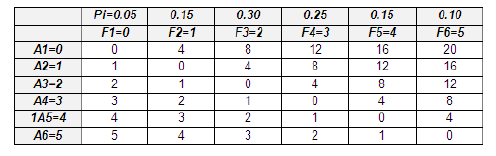
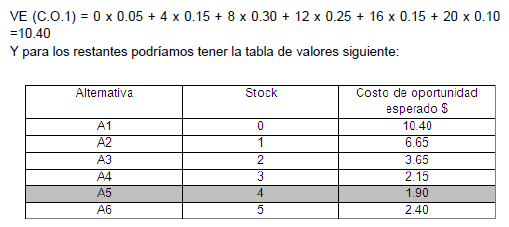
En nuestro caso específico, el Valor Esperado del costo de oportunidad para la alternativa A5 se puede calcular de la siguiente manera: VE(CO5) = GIC - VE(A5) = $10,40 - $8,50 = $1,90. Debido a nuestro enfoque en minimizar los costos de oportunidad, es lógico elegir una vez más la alternativa A5 como la opción adecuada. El valor mínimo del costo de oportunidad se conoce como Costo de Riesgo, el cual representa la pérdida inevitable asociada a la toma de decisiones en condiciones de riesgo. Para ilustrar esto, si implementamos una estrategia que coincida con el valor de la demanda, lograríamos lo que llamamos Ganancia con Información Completa (GIC). El GIC se puede calcular multiplicando cada valor de demanda por su probabilidad correspondiente y sumándolos. En nuestro ejemplo, el GIC es $10,40. En términos generales, podemos expresar el Valor Esperado (EV) del costo de oportunidad de una determinada estrategia como la diferencia entre el beneficio esperado con información completa y el valor esperado del beneficio para esa alternativa. En discusiones anteriores, tocamos el valor del costo del riesgo, que representa la pérdida de ganancias que se incurre al tomar decisiones en condiciones inciertas en lugar de tener total certeza. Este costo también equivale al valor de la información adicional.
Para decirlo de otra manera, la disposición del comerciante a pagar por la información adicional no excedería los 1,90 dólares. Esto se debe a que el incremento potencial en las ganancias que se pueden lograr a través de esa información adicional está valorado en $1,90, y sería ilógico que el comerciante pagara una cantidad que excederá el beneficio que se derivaría de ello.
El valor de un nodo dentro del árbol se puede calcular una vez que se conocen todos los valores de los nodos posteriores, el valor de un nodo de decisión se determina seleccionando el valor más alto entre todos los nodos inmediatamente posteriores. Mientras tanto, el valor de un nodo de probabilidad se determina calculando el valor esperado en función de los valores de los nodos posteriores, teniendo en cuenta las probabilidades asociadas a cada rama. Al atravesar el árbol desde las ramas hasta la raíz, se pueden calcular los valores de todos los nodos, incluida la raíz del árbol. La incorporación de estos resultados numéricos al árbol de decisiones produce una representación gráfica completa del proceso de toma de decisiones.
El árbol de decisiones sirve como representación visual del proceso cronológico de toma de decisiones, se construye utilizando dos tipos de nodos: nodos de decisión, que se representan como cuadrados que representan elecciones, y nodos de estados de la naturaleza, que se representan mediante círculos que indican probabilidades para crear un árbol de decisiones, primero se debe delinear el flujo lógico del problema. Para los nodos de probabilidad, es crucial asegurarse de que las probabilidades asignadas a cada rama sumen uno, al atravesar el árbol de derecha a izquierda, se pueden calcular los beneficios esperados evaluando cada nodo de forma inversa.
Supongamos que una organización se enfrenta a la tarea de decidir si contrata o no a un consultor que cobra unos honorarios de 500 dólares para pedirle asesoramiento sobre si proceder o no con la producción de un producto. Para ayudar a tomar esta decisión, se construye un árbol de decisiones que presenta tres opciones posibles: no contratar al consultor, pagar la tarifa de $500 por sus servicios o contratar al consultor. Después de una evaluación y análisis exhaustivos del árbol de decisiones, resulta evidente que el curso de acción más favorable es contratar al consultor y esperar pacientemente su informe.
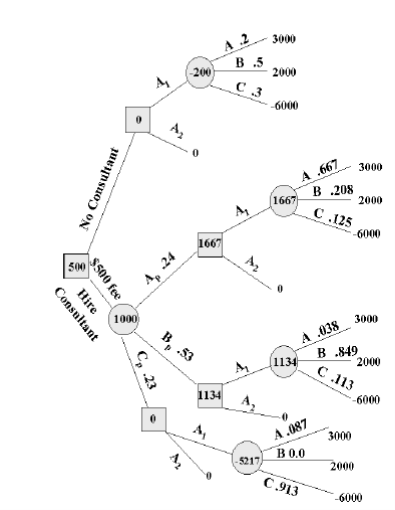
Para abordar el problema desde una perspectiva diferente, se reconsidera el escenario utilizando una distribución previa plana, esto significa que se asignan probabilidades iguales a cada resultado, a diferencia de la distribución anterior de (0,2, 0,5, 0,3) que representaba la probabilidad de diferentes niveles de ventas. En este caso, el propietario del problema no tiene ningún conocimiento sobre el nivel potencial de ventas si el producto se introduce en el mercado. En última instancia, el árbol de decisiones demuestra ser un método eficaz para tomar decisiones por varias razones. En primer lugar, permite una visualización clara del problema, permitiendo tener en cuenta todas las opciones disponibles, facilita un análisis exhaustivo de las posibles consecuencias derivadas de diferentes decisiones, los árboles de decisión proporcionan un marco para cuantificar los valores de los resultados y las probabilidades asociadas con su logro. Esto ayuda a tomar mejores decisiones basadas en la información existente y mejora la precisión de los pronósticos. Para evaluar la eficiencia del consultor se calcula un índice dividiendo el beneficio esperado obtenido de su asesoramiento por el VEIP (Valor de la Información Previa Esperada). El beneficio esperado derivado del uso del consultor se calcula como $1000 - $500 = $500. Por otro lado, el VEIP se calcula como 0,2(3000) + 0,5(2000) + 0,3(0) = 1600. Por lo tanto, se determina que la eficiencia del consultor es 500/1600, lo que se traduce en 31%.
La Aplicabilidad en este análisis integral ayudará al equipo directivo superior de ABC a tomar decisiones informadas con respecto a su línea de productos, asegurando la maximización de las ganancias netas. ABC, una empresa a la que nos referiremos como ABC por simplicidad, ha creado recientemente una nueva gama de productos. Los altos mandos de la empresa están interesados en determinar la estrategia más adecuada que incorpore tanto Marketing como Producción. En este análisis, consideraremos tres estrategias potenciales, a saber, A, B y C, cada una de las cuales posee características distintas, la estrategia A se etiqueta como agresiva, la estrategia B como básica y la estrategia C como cuidadosa.
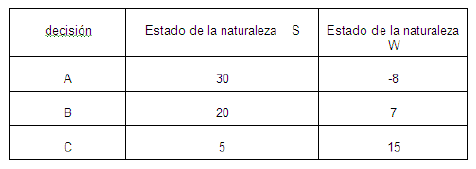
Según las estimaciones de la dirección, existe un 45% de posibilidades de tener un mercado S y un 55% de posibilidades de tener un mercado W.
El proceso de utilizar un árbol de decisión para determinar la decisión óptima se denomina resolución del árbol. Para solucionar el árbol se debe trabajar desde el final hacia el principio, lo que se conoce como poda del árbol. Inicialmente, las ramas terminales se rastrean calculando un valor esperado para cada nodo terminal, como se muestra en el Gráfico 2.4. Un método más conveniente para representar este problema es mediante el uso de árboles de decisión, como se muestra en el gráfico adjunto. En este enfoque, los nodos cuadrados se utilizan para indicar puntos donde es necesario tomar decisiones, y cada línea que emana del cuadrado representa una decisión potencial. Por otro lado, los nodos circulares se utilizan para representar situaciones en las que el resultado es incierto y cada línea que sale del círculo significa un posible evento.
Gráfico 2.4
Decisión para ABC
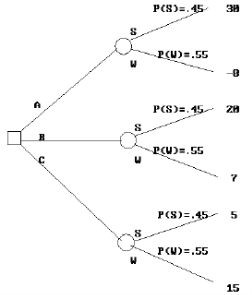
Gráfico 2.5
Árbol de decisión reducido para ABC
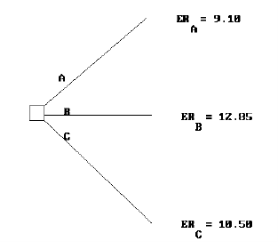
La tarea de la administración es abordar una cuestión menos compleja, que pasa por seleccionar la opción que resulte en el mayor valor previsto al final del proceso. Al utilizar un árbol de decisión, el problema se puede visualizar de una manera más ilustrativa. Se emplean los mismos datos y cálculos que antes.
Por lo tanto, el valor anticipado es una ecuación lineal que depende de la probabilidad de que las circunstancias del mercado sean sólidas. De manera similar, el valor esperado se puede expresar como una función lineal basada en la probabilidad de condiciones favorables del mercado.
Las tres funciones lineales se pueden representar en el mismo plano de coordenadas, como se muestra en la Gráfico 2.6
Gráfico 2.6
Valor esperado en función de P(S)
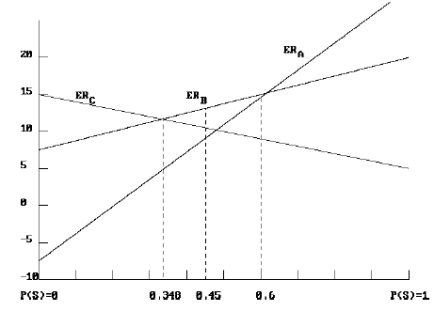
El diagrama indica claramente que ABC debería optar por la estrategia B, conocida como estrategia básica, cuando la probabilidad de una demanda fuerte cae dentro del rango de P(S)=0,348 a P(S)=0,6. Sin embargo, si la probabilidad de una demanda fuerte cae por debajo de 0,348, sería más ventajoso seleccionar la estrategia C. Por el contrario, si la probabilidad de una demanda fuerte supera 0,6, sería óptimo elegir la estrategia agresiva A.
Por otro lado, cuando las condiciones del mercado eran débiles (etiquetadas como W), los estudios tendían a ser desalentadores el 70% de las veces. Esto sugiere que durante tiempos de debilidad del mercado, los estudios a menudo resaltaron obstáculos o riesgos potenciales asociados con la estrategia. Al analizar estos factores, podemos obtener una comprensión más clara de las implicaciones de consultar al grupo de Investigación de Mercados. El costo del estudio debe sopesarse frente a los beneficios potenciales de recibir ideas alentadoras o desalentadoras.
En última instancia, esta información guiará a la gerencia en la toma de decisiones estratégicas que se alineen con las metas y objetivos de la empresa. En el pasado, estos estudios han demostrado ser bastante fiables. Cuando las condiciones del mercado eran desafiantes (etiquetadas como S), los estudios eran alentadores el 60% de las veces y desalentadores el 40% de las veces. Esto indica que la mayoría de las veces, los estudios proporcionaron información positiva, infundiendo confianza en la estrategia. Para proporcionar una comprensión más completa del problema, profundicemos en una aplicación detallada utilizando un ejemplo. En este escenario, redefiniremos el problema considerando la estrategia B y la posible participación del grupo de Investigación de Mercados de la empresa. Se puede consultar a este grupo para obtener información sobre la viabilidad de la estrategia. En el lapso de un mes, el grupo de Investigación de Mercado proporcionará una indicación de si los resultados del estudio son alentadores (etiquetados como E) o desalentadores (etiquetados como D). Es importante considerar también el aspecto financiero. Realizar un estudio de esta naturaleza tiene un costo de 500.000 dólares. Esta inversión es necesaria para recopilar la información necesaria y tomar decisiones informadas con respecto a la implementación de la estrategia B.
Gráfico 2.7
Decisiones Secuenciales.
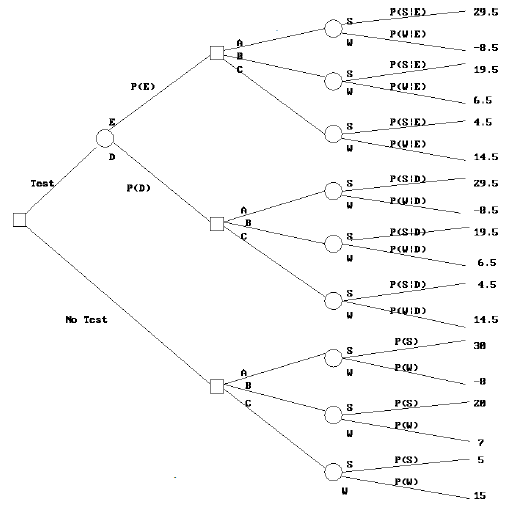
La cuestión que nos ocupa es si la dirección debería o no emprender un estudio similar al que se está examinando. Para tomar esta decisión, es necesario construir un árbol de decisión que describa los pasos secuenciales involucrados. Este árbol de decisión, que se muestra en la Gráfico 2.8, se crea en el orden en que la información relevante esté disponible. El primer nodo en el lado izquierdo del árbol representa la decisión de realizar o no la prueba. Siguiendo la rama "Prueba", el siguiente nodo a la derecha se representa como un círculo, lo que indica un evento incierto. Este evento puede tener uno de dos resultados posibles: la prueba puede ser motivadora (E) o desmotivadora (D). Es necesario calcular las probabilidades de estos resultados, denotadas como P(E) y P(D) respectivamente. Para calcular estas probabilidades, es fundamental comprender el concepto de probabilidades condicionales. La información dada es condicional, lo que significa que las probabilidades dependen de ciertas condiciones. Por ejemplo, dada la condición S, la probabilidad de que la prueba sea motivadora (E) es del 60%, mientras que la probabilidad de que sea desmotivadora (D) es del 40%. De manera similar, dada la condición W, la probabilidad de E es del 30% y la probabilidad de D es del 70%. Estas probabilidades condicionales se pueden expresar como ecuaciones matemáticas.
A medida que avanzamos hacia el lado derecho del árbol de decisiones, encontramos nodos de forma cuadrada que representan tres estrategias de marketing y producción distintas. Continuando hacia la derecha, nos encontramos con nodos circulares que indican las condiciones inciertas del mercado, ya sea débil o fuerte. La ocurrencia de estos eventos ahora depende de los eventos inciertos que tuvieron lugar antes, como los resultados del estudio de mercado realizado en ese momento, en consecuencia, se hace necesario calcular las probabilidades condicionales asociadas con estos eventos.
Ahora estamos preparados para resolver el árbol de decisiones. Al igual que antes, este proceso se lleva a cabo de manera inversa, comenzando desde el final. Consulte las figuras 5, 6 y 7 para obtener una representación visual. Al retroceder desde un nodo circular, calculamos los valores esperados. Al elegir la decisión con el valor esperado más alto, retrocedemos desde un nodo cuadrado. El valor esperado al realizar un estudio de mercado se determina que es de 12.96 millones de dólares, superando el valor esperado sin el estudio. Por tanto, es necesario realizar el estudio. Por último, compararemos el valor esperado del estudio (denominado EVSI) con el valor esperado de la información de la muestra, denominado valor esperado de la información de la muestra (EVSI). Esto se contrastará con el valor esperado de información perfecta (EVPI) VEIP.
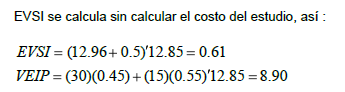
Es evidente que la investigación de mercado carece de eficacia, como lo demuestra la importante disparidad entre los valores EVSI y EVPI, considerando que su valor esperado de información perfecta (EVSI) es mayor que su costo asociado, sería prudente proceder con esta acción.
Gráfico 2.8
Estructurando el Árbol
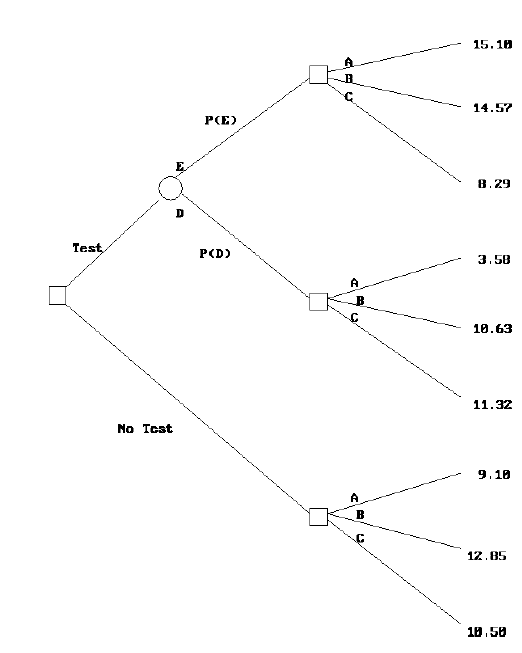
CAPÍTULO III
3. PROGRAMACIÓN LINEAL
En 1941-1942, se formuló formalmente por primera vez el problema del transporte, estudiado independientemente por Koopmans y Kantarovitch. Este problema, a menudo denominado problema de Koopmans-Kantarovitch, marcó un hito importante en el desarrollo de la programación lineal. Apenas tres años después, G. Stigler introdujo otro problema notable conocido como la dieta óptima. Durante los siglos XVII y XVIII, el campo de las matemáticas fue testigo de las notables contribuciones de matemáticos de renombre como Newton, Leibnitz, Bernouilli y Lagrange. Estos genios matemáticos desempeñaron un papel crucial en el desarrollo del cálculo infinitesimal y se centraron particularmente en la obtención de máximos y mínimos condicionales de diversas funciones.
En 1947, G.B. Dantzig formuló la afirmación matemática estándar a la que se podría reducir todo problema de programación lineal. Esta formulación, junto con los esfuerzos del grupo SCOOP (Scientific Computation of Optimum Programs), del que formaba parte Dantzig, propició la aplicación de la programación lineal en diversos campos, particularmente en las operaciones militares. El puente aéreo de Berlín fue una de las primeras aplicaciones reales de los estudios del grupo SCOOP. Con el paso del tiempo, un matemático francés llamado Jean Baptiste-Joseph Fourier (1768-1830) hizo los primeros intentos intuitivos pero imprecisos de lo que ahora llamamos programación lineal. Sin embargo, no fue hasta 1776, cuando Gaspar Monge (1746-1818) se interesó por problemas similares, que se produjeron mayores avances en este campo. Avance rápido hasta 1939, cuando un matemático ruso llamado Leonidas Vitalyevich Kantarovitch publicó una monografía completa titulada "Métodos matemáticos de organización y planificación de la producción".
Este trabajo innovador presentó una teoría matemática precisa y bien definida que esencialmente allanó el camino para lo que ahora conocemos como programación lineal. Una de las primeras aplicaciones prácticas de los métodos de programación lineal se produjo en 1858, cuando se utilizaron para calcular el plan óptimo para transportar arena de construcción a varias obras de construcción en Moscú. Este plan de transporte, calculado usando la computadora Strena durante un período de 10 días en junio, resultó en una reducción de gastos del 11% en comparación con los costos anticipados.
El método simplex, un algoritmo ampliamente utilizado en programación lineal, fue estudiado por primera vez en 1951 por Dantzig en la Oficina de Estándares SEAC COMPUTER de los Estados Unidos. Dantzig utilizó varios modelos informáticos de la empresa IBM en su investigación. En la era posterior a la Segunda Guerra Mundial, Estados Unidos reconoció la necesidad de una coordinación y optimización efectivas de los recursos de la nación. Los modelos de programación lineal se consideraron una solución a este complejo problema. Al mismo tiempo, los avances en las técnicas informáticas y en las propias computadoras proporcionaron los medios para resolver y simplificar estos problemas emergentes.
Alrededor de 1950, se formaron varios grupos de estudio en los Estados Unidos para explorar y desarrollar diferentes aspectos de la programación lineal. Estos grupos incluían la Rand Corporation, el Departamento de Matemáticas de la Universidad de Princeton y la Escuela de Graduados en Administración Industrial Carnegie del Instituto de Tecnología. Los principios matemáticos fundamentales de la programación lineal se pueden atribuir a Janos von Neuman, un matemático estadounidense de origen húngaro. En su famosa obra "Teoría de juegos", publicada en 1928, von Neuman sentó las bases de la programación lineal. En 1947, conjeturó la equivalencia entre los problemas de programación lineal y la teoría de matrices, despertando aún más el interés entre los investigadores por el desarrollo riguroso de esta disciplina.
Para el problema 1), designemos el número de bolsas de alimento de clase P como x y el número de bolsas de alimento de clase Q como y. La función Z = 300x + 800y representa el ingreso total obtenido por la venta de bolsas, por lo que esta es la cantidad que debemos maximizar. Una campaña promocional de una marca de productos lácteos se centra en la distribución gratuita de yogures con sabor a limón o fresa. El objetivo es distribuir al menos 30.000 yogures. Cada yogur de limón requiere 0,5 gramos de un producto de fermentación, mientras que cada yogur de fresa requiere 0,2 gramos del mismo producto. Hay 9 kilogramos de este producto de fermentación disponibles para su uso. El costo de producción de un yogur de limón es de $30 y el de un yogur de fresa es de $20. En ambos ejemplos, está claro qué cantidad pretendemos maximizar o minimizar.
Estas cantidades se pueden expresar en forma de ecuaciones lineales, las restricciones planteadas por las condiciones dadas en ambos problemas pueden expresarse como desigualdades lineales. En diversos campos como la industria, la economía y la estrategia militar, existen numerosas situaciones en las que se hace necesario optimizar o minimizar determinadas funciones que están sujetas a restricciones específicas, a las que nos referiremos como restricciones. En una granja, hay dos tipos de alimento, P y Q, que se producen mezclando dos productos, A y B. Cada bolsa de alimento P contiene 8 kg de A y 2 kg de B, mientras que cada bolsa de alimento Q contiene 10 kg de A y 5 kg de B. El precio de venta de cada bolsa de P es de $300 y de cada bolsa de Q es de $800. Si hay 80 kg de A y 25 kg de B disponibles en la granja, ¿cuántas bolsas de cada tipo de alimento se deben producir para maximizar los ingresos? Ejemplo 2: Problema de minimización. Ejemplo 1: problema de maximización.
Para ayudarnos a determinar las limitaciones, podemos crear una tabla compacta que describa la información necesaria.
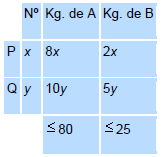
Por el contrario, es lógico suponer que las variables xy no pueden tener valores negativos, lo que implica que deben ser no negativos.
Tenemos una colección de limitaciones que se pueden representar como el producto de 8 y una variable x.
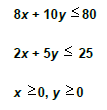
En el problema 2, asignemos la variable "x" para representar la cantidad de yogures de limón e "y" para representar la cantidad de yogures de fresa. Entonces podemos definir la función de costos como Z = 30x + 20y, es importante señalar que las condiciones del problema imponen ciertas restricciones que debemos considerar.
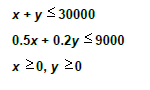
Una formulación estándar de un problema de programación lineal en dos variables es la siguiente.
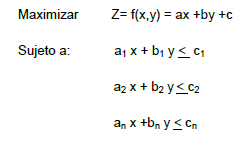
El conjunto de valores de xy que satisfacen todas las restricciones se conoce como conjunto o región factible. Cada punto dentro de este conjunto tiene el potencial de ser una solución al problema, mientras que cualquier punto fuera de él no puede ser una solución. En la siguiente sección, exploraremos cómo determinar la región factible. La solución óptima al problema es un par de valores (x0, y0) que pertenecen al conjunto factible y hacen que la función objetivo f(xy) alcance el valor máximo o mínimo. Las restricciones, que son desigualdades lineales, están determinadas por las limitaciones, disponibilidades o necesidades del problema. El número de restricciones puede variar según el problema específico. Estas desigualdades pueden ser de la forma "menor que" (representado por < o ≤) o "al menos" (representado por > o ≥). La dirección de las desigualdades depende de si el problema es maximizador o minimizador. Un problema de programación lineal en dos variables implica encontrar la solución óptima para una función objetivo dada y un conjunto de restricciones. La función objetivo, denotada como f(xy), es una combinación lineal de las variables de decisión x e y, multiplicadas por las constantes a y b, con una constante adicional c. El objetivo es maximizar o minimizar esta función objetivo.
3.1 Determinación de la región Factible.
Si un problema de programación lineal tiene solución, ésta debe estar dentro de los límites definidos por las diversas desigualdades. Esta área se conoce como región factible y puede tener límites o no.
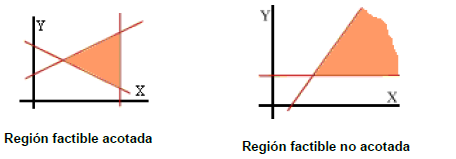
El proceso para determinar la región factible es el siguiente. En el caso de que la región factible sea limitada, su representación gráfica será un polígono convexo con un número de lados menor o igual al número de restricciones. La región factible consta de los lados y vértices de un polígono, y si estos están incluidos o no depende de si las desigualdades son en sentido amplio o estricto.
Al igual que los sistemas de ecuaciones lineales, los sistemas de desigualdades lineales pueden tener varias posibilidades para sus soluciones. Puede que no haya solución y, si la hay, el conjunto de soluciones puede ser acotado o ilimitado. Luego, la región factible se forma encontrando la intersección o región común de todas las soluciones de las desigualdades. Para determinar la región factible, cada desigualdad se resuelve por separado, lo que da como resultado un semiplano de soluciones. Se traza la recta asociada a cada desigualdad, dividiendo el plano en dos regiones o semiplanos. Para identificar la región válida, se selecciona un punto (como (0,0)) y se verifican sus coordenadas para ver si satisfacen la desigualdad. Si es así, la región que contiene ese punto es la región válida; de lo contrario, la otra región es válida. La región factible en un problema de programación lineal puede incluir o excluir los lados y vértices, dependiendo de si las desigualdades son inclusivas o estrictas. Cuando la región factible está acotada, se representa gráficamente como un polígono convexo con un número de lados igual o menor que el número de restricciones del problema.
Para ilustrar mejor este concepto, consideremos un ejemplo en el que necesitamos dibujar la región factible asociada con ciertas restricciones.
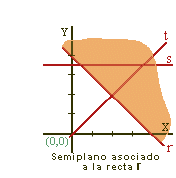
Seleccionamos como punto de referencia el punto O(0,0), situado en el semiplano que se encuentra debajo de la recta. Al sustituir las coordenadas (0,0) en la desigualdad x + y < 4, se hace evidente que el punto no satisface la desigualdad: 0 + 0 = 0, que es menor que 4. En consecuencia, el conjunto de soluciones a la desigualdad constituye el semiplano situado encima de la recta r, representado por la ecuación x + y = 4.
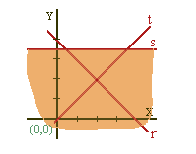
En el siguiente paso, seguimos el mismo procedimiento que hicimos en el paso anterior. La desigualdad se satisface con las coordenadas (0,0) y con 4 (0,4). Esto significa que el conjunto de soluciones de la desigualdad es el semiplano que incluye el punto O.
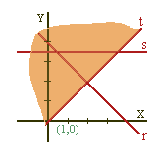
La recta t que está relacionada con la restricción pasa por el origen. Esto implica que si usáramos el punto O(0,0), no podríamos sacar ninguna conclusión. En lugar de ello, seleccionamos el punto (1,0) y determinamos que no cumple los requisitos de la desigualdad y x (y = 0 < 1 = x). Por tanto, el conjunto solución para esta desigualdad consiste en el semiplano definido por la recta t, excluyendo el punto (1,0).
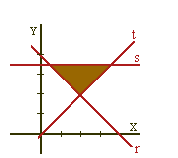
La región factible está creada por los puntos que satisfacen las tres restricciones, lo que significa que están situados dentro de los tres semiplanos anteriores.
3.2 Método Gráfico.
Por ejemplo, si tenemos una función objetivo f(xy) = ax + by + c, la ecuación de las líneas de nivel tendrá la forma ax + by + c = 0 o ax + by = k. Al cambiar el valor de k, podemos obtener diferentes niveles para estas rectas y, en consecuencia, diferentes valores para f(x,y). Ahora bien, cuando se trata de resolver un problema de programación lineal, los únicos puntos de interés son aquellos dentro de la región factible. Esta es la región que satisface todas las restricciones dadas. En este contexto, las únicas líneas de nivel que importan son las que intersectan o tocan la región factible. A medida que aumentamos o disminuimos el valor de k y movemos estas líneas, el máximo o mínimo de la función objetivo f(x,y) se alcanzará en el último o primer punto de contacto entre estas líneas y la región factible. Es importante señalar que en un problema de programación lineal, todas las líneas de nivel son paralelas, esto se debe a que los coeficientes a y b de la recta ax + by = k determinan su pendiente.
Por lo tanto, si tenemos dos valores diferentes de k, digamos k1 y k2, las rectas ax + by = k1 y ax + by = k2 serán paralelas. Esto significa que una vez que dibujamos una de estas líneas, podemos obtener el resto desplazándolas de forma paralela. El concepto de líneas de nivel es fundamental para comprender cómo resolver problemas de programación lineal. Estas líneas representan los puntos en un plano donde la función objetivo toma el mismo valor. Es decir, nos muestran los diferentes valores que puede tener la función objetivo. En resumen, el concepto de líneas de nivel es crucial para resolver problemas de programación lineal. Nos ayudan a comprender los diferentes valores que puede tener la función objetivo y nos orientan a encontrar el máximo o mínimo dentro de la región factible. Al manipular las líneas de nivel, podemos determinar la solución óptima al problema en cuestión.
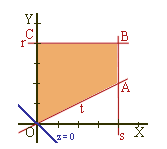
A medida que aumentamos o disminuimos el nivel de estas líneas, el valor máximo o mínimo de la función objetivo f(x,y) se alcanzará en el último o primer punto de contacto entre las líneas de nivel y la región factible. Esta observación proporciona una visión valiosa del proceso de optimización de problemas de programación lineal. Para ser más específicos, consideremos una función objetivo de la forma f(x,y) = ax + by + c, donde a, b y c son constantes. La ecuación de las líneas de nivel se puede escribir como ax + by + c = 0 o ax + by = k, donde k representa un valor constante. Al ajustar el valor de k, podemos obtener diferentes niveles para estas líneas, lo que resulta en diferentes valores para f(x,y). Sin embargo, en el contexto de la resolución de un problema de programación lineal, no todas las líneas de nivel son igualmente importantes.
Los únicos puntos de interés son aquellos que se encuentran dentro de la región factible, que representa el conjunto de todas las soluciones válidas que satisfacen las restricciones dadas. En consecuencia, sólo son relevantes las líneas de nivel que están en contacto con la región factible, las líneas de nivel juegan un papel crucial en la comprensión del comportamiento de la función objetivo en un problema de programación lineal. Estas líneas representan los puntos del plano en los que la función objetivo toma el mismo valor. Al manipular la ecuación de las líneas de nivel, podemos explorar diferentes valores de la función objetivo variando el término constante.
Vale la pena señalar que en un problema de programación lineal, todas las líneas de nivel son paralelas entre sí. Esto se debe a que los coeficientes a y b de la ecuación ax + by = k determinan la pendiente de estas rectas. Por lo tanto, si tenemos dos constantes diferentes k1 y k2, las rectas ax + by = k1 y ax + by = k2 serán paralelas entre sí. Esta propiedad nos permite generar fácilmente líneas de nivel adicionales simplemente desplazándolas paralelas a cualquier línea existente. En resumen, el concepto de líneas de nivel es una herramienta poderosa para resolver problemas de programación lineal. Al manipular la ecuación de estas rectas y examinar sus intersecciones con la región factible, podemos determinar las soluciones óptimas que maximizan o minimizan la función objetivo.
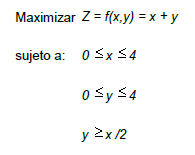
Resolviendo los sistemas de ecuaciones que corresponden al problema, podemos calcular los vértices de la región factible.
Representamos las líneas que indican diferentes niveles o alturas.
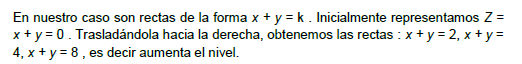
La Solución óptima:
Hay tres distribuciones de probabilidad comunes que se utilizan para representar los tiempos de llegada y servicio: Markov (generación de Poisson), determinista y general. La distribución de Markov, que lleva el nombre del matemático A.A. Markov, se utiliza para describir eventos aleatorios que carecen de memoria de eventos pasados. Una distribución determinista representa eventos que ocurren a un ritmo constante sin ningún cambio. La distribución general abarca cualquier otra distribución de probabilidad que pueda describir el patrón de llegadas y servicios. Para describir eficientemente los parámetros de un sistema de cola de espera, Kendall desarrolló un sistema de notación. En notación Kendall, los tiempos de espera en un sistema de líneas se designan mediante símbolos específicos. Las tarifas de llegada y de servicio suelen ser inciertas y pueden describirse mediante distribuciones de probabilidad.
La notación Kendall es un sistema de clasificación que utiliza varias letras para representar diferentes características de un sistema de colas. Por ejemplo, la letra M se utiliza para indicar un proceso markoviano, D significa un proceso determinista y G representa un proceso general. Para ilustrar esta notación, consideremos un sistema de cola de espera que implica llegadas aleatorias, servicio determinista y tres canales de servicio. En la notación de Kendall, este sistema específico se identificaría de la siguiente manera.
En cada escenario, se supone que solo hay una línea de entrada, es importante reconocer que hay factores adicionales que deben considerarse. Estos incluyen el tamaño de la población de donde provienen los elementos que ingresan al sistema de línea de espera, la forma en que llegan las unidades (individualmente o en grupos), la posibilidad de que las unidades rechacen el sistema debido a largos tiempos de espera, la posibilidad de que las unidades abandonen el sistema. sistema después de esperar un cierto período, y si hay suficiente espacio para que todas las unidades que lleguen esperen en la fila. Ahora, profundicemos en los diferentes modelos de Línea de Espera que se analizarán.
El sistema bajo consideración involucra una distribución de llegadas Markoviana, un tiempo de servicio Markoviano y un servidor. Esto significa que las llegadas siguen un patrón determinado y los horarios de servicio también siguen una distribución específica. El sistema está diseñado para manejar llegadas aleatorias, que se pueden observar comúnmente en diversos escenarios cotidianos. Un ejemplo clásico de llegadas aleatorias son las llamadas entrantes recibidas por una central telefónica o un servicio de emergencia. En segundo lugar, la probabilidad de una llegada durante un período de tiempo específico está determinada únicamente por la duración del intervalo y no por el momento en que ocurre el período. A este concepto se le suele denominar falta de “memoria” en estos sucesos. Al conocer el número promedio de llegadas por período, podemos calcular las probabilidades de que ocurran diferentes números de eventos dentro de ese período. Esto es posible utilizando las probabilidades conocidas proporcionadas por la distribución de Poisson. Para ser más específicos, si hay un promedio de l llegadas dentro de un período T determinado, podemos determinar la probabilidad de tener n llegadas dentro del mismo período utilizando los cálculos apropiados basados en la distribución de Poisson. Esto nos permite comprender y analizar mejor el comportamiento de las llegadas aleatorias al sistema.
Existe una diferencia entre llegadas aleatorias y horarios de servicio aleatorios. Mientras que las llegadas aleatorias se describen mediante una distribución de Poisson discreta, los tiempos de servicio aleatorios se describen mediante una distribución continua. En particular, la duración de los tiempos de servicio suele modelarse utilizando una distribución exponencial con un parámetro negativo. Se elige esta distribución porque representa con precisión la naturaleza aleatoria de los tiempos de servicio. En situaciones donde las colas de espera son comunes, la aparición de horarios de servicio aleatorios también es bastante común. Al igual que en las llegadas aleatorias, los tiempos que tardan en completarse los servicios son impredecibles y no tienen ningún recuerdo de sucesos anteriores. Estos tiempos de servicio se describen mediante una distribución de probabilidad, al igual que las llegadas aleatorias. Si la tasa promedio a la que se completan los servicios se denota por m, entonces la distribución de los tiempos de servicio se puede determinar utilizando la fórmula de distribución exponencial.
Esta fórmula se puede utilizar para determinar la probabilidad de que el servicio exceda una duración de tiempo específica, denominada T. El diagrama adjunto ilustra el modelo al que se hace referencia.
3.5 Características de las Operaciones Deterministas.
Para comprender mejor la utilización del sistema, podemos introducir el concepto de factor de utilización, denotado como r. Este factor representa la fracción promedio de tiempo que el sistema está ocupado y el número promedio de unidades atendidas en un momento dado. En otras palabras, r puede verse como una medida de la eficiencia del sistema. Para calcular las características operativas de una cola M/M/1, es importante considerar varios factores. En primer lugar, se deben observar la tasa media de llegada, denotada como λ, y la tasa media de servicio, denotada como μ, es fundamental tener en cuenta que la tasa de llegada debe ser menor que la tasa de servicio (λ < μ). Si no se cumple esta condición, el número promedio de llegadas excedería el número promedio de unidades atendidas, lo que resultaría en un número infinito de unidades esperando en la cola. Para calcular las características operativas de la cola M/M/1 en términos de probabilidad, es necesario considerar varias probabilidades relacionadas con el sistema. Estas probabilidades incluyen la probabilidad de tener cero unidades en el sistema, la probabilidad de tener exactamente una unidad en el sistema y la probabilidad de tener múltiples unidades en el sistema. Al analizar estas probabilidades, podemos obtener información sobre el comportamiento y el rendimiento de la cola M/M/1.
Entonces la probabilidad de que el sistema no esté funcionando o esté vacío es P0, puedes obtenerlo de:
De esto podemos obtener la probabilidad de que existan n unidades. Sistema, Pn, Autor:
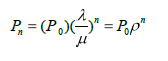
Este importante hallazgo nos permite determinar las propiedades operativas de las colas. Una de las principales propiedades operativas que evaluamos es la cantidad media de entidades presentes en el sistema, que incluye tanto las que están en espera como las que reciben servicio. Esta cantidad media se conoce como número promedio de unidades, denotada como L. En consecuencia, necesitamos...
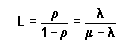
Utilizando los valores que hemos recopilado, podemos calcular la cantidad promedio de unidades que se encuentran actualmente en estado de espera, denominada Lq. L representa el recuento total de unidades que están esperando o siendo atendidas, mientras que r significa la cantidad promedio de unidades que están siendo atendidas en un momento específico.
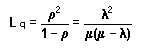
Ahora examinaremos el tiempo de espera. Usaremos W para representar el tiempo promedio o tiempo esperado de una unidad en el sistema. Para encontrar W, observaremos que si L es el número esperado de unidades en el sistema y l es el número promedio de unidades que llegan para recibir servicio en cada período, entonces el tiempo promedio que cualquier unidad que llega debe estar en el sistema está dado por :
De manera similar, el tiempo esperado o promedio que una unidad debe esperar para recibir servicio, Wq, está dado por:
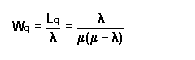
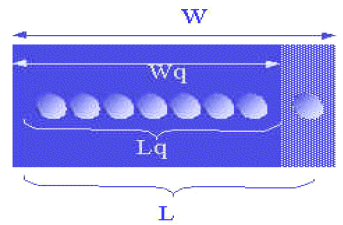
Una fila de espera recibe 20 unidades cada hora, mientras que el tiempo promedio que tarda en atender cada unidad es de 30 unidades por hora. Realicemos un análisis de esta fila de espera.
Según la información proporcionada anteriormente, podemos determinar la probabilidad de que el sistema esté ocupado o activado.
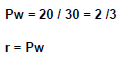
Luego, existe la probabilidad de que el sistema no esté ocupado u ocupado con otras tareas.
El número esperado de unidades en el sistema está definido por:
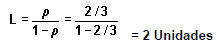
El número de unidades en espera de ser atendidas se puede determinar considerando el valor esperado.
En promedio, habrá una mayor cantidad de unidades en espera de ser atendidas en comparación con la cantidad de unidades que actualmente reciben servicio. Específicamente, por cada tres unidades en servicio, habrá cuatro unidades esperando ser atendidas.
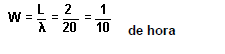
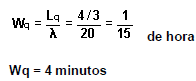
Cuando se trata de determinar las características de la línea de espera para el modelo M/M/S, los cálculos son ligeramente más complejos en comparación con el caso del canal único. Sin embargo, nuestro enfoque principal es comprender las implicaciones de estas características en lugar de las fórmulas específicas necesarias para calcularlas. Por lo tanto, nos basaremos en tablas que se han preparado utilizando estas fórmulas para simplificar los cálculos. Este modelo particular se basa en el supuesto de que las llegadas y los horarios de servicio son aleatorios para múltiples canales de servicio. Comparte las mismas consideraciones que el modelo de canal de servicio único (M/M/1), con la única diferencia de la presencia de una única cola de entrada que suministra los múltiples canales de servicio. Las tarifas de servicio para todos los canales son iguales.
3.7 características del Modelo M/M/S
En el modelo M/M/S ya no es necesario que la tarifa promedio de servicio (m) sea mayor que la tasa de llegada (l), pero sí es importante que el producto de la tarifa promedio de servicio por el número de servicios Los canales (Sm) deben ser mayores que la tasa de llegada para evitar una acumulación interminable de colas de espera. En el escenario M/M/S, la característica clave utilizada para cálculos adicionales es la probabilidad de que el sistema esté ocupado. Esta probabilidad representa la posibilidad de tener S o más unidades en el sistema, lo que indica que todos los canales de servicio están siendo utilizados y por lo tanto el sistema se considera ocupado.
Al utilizar las ecuaciones antes mencionadas, podemos determinar la información adicional necesaria para el sistema. De manera similar al modelo M/M/1, en el modelo M/M/S podemos expresar L como la suma de Lq y r. Sin embargo, en este caso, utilizaremos el valor P, que representa la proporción de tiempo que el sistema está ocupado, para calcular Lq.
Figura 3.1 se representa el Modelo
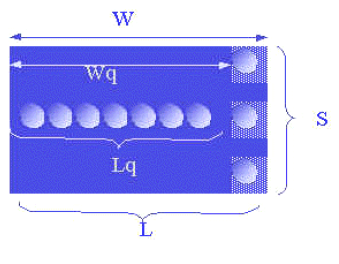
Para proporcionar una ilustración clara del modelo M/M/S, consideremos un escenario donde hay cinco canales de servicio. En este caso, la tasa de servicio promedio, denotada como μ, se fija en 6. Además, la tasa de llegada de unidades que buscan servicio es de 24 por hora. Dados estos valores, podemos deducir que el número de servidores, representado por S, es igual a 5.
Para agilizar el proceso de búsqueda de los valores de Po podemos hacer uso de una tabla auxiliar que está integrada en este sistema. Esta tabla nos proporciona convenientemente el valor necesario teniendo en cuenta los valores de S (el número de servidores) y r (la tasa de llegada). Consultando esta tabla podemos determinar que el valor de Po es igual a 0,0130, podemos calcular la probabilidad de que el sistema esté ocupado, denotada como P (sistema ocupado), que asciende a 0,5547. Utilizando esta valiosa información, podemos deducir además que...
El sistema de colas de espera descrito en este modelo se caracteriza por llegadas aleatorias y una distribución general de los tiempos de servicio. Los tiempos de servicio en este sistema siguen una distribución cuya desviación estándar se supone conocida. El sistema consta de un canal de atención y una fila de espera. Al igual que en casos anteriores, las llegadas en este modelo se distribuyen según una distribución de Poisson, a diferencia de casos anteriores, los tiempos de servicio no siguen una distribución específica como la distribución exponencial.
Podemos considerar el caso M/G/1 porque las fórmulas utilizadas para calcular sus características operativas son relativamente sencillas. Sin embargo, al igual que en el caso M/M/S, no es posible calcular directamente el número esperado de unidades en el sistema (L). En lugar de ello, primero debemos calcular el número de unidades en espera de ser atendidas (Lq) y luego usar esta información para determinar el valor de L. Para calcular Lq, necesitamos conocer la desviación estándar de la distribución que representa la tiempos de servicio. Sin conocimiento de la distribución de los tiempos de servicio, es imposible determinar con precisión las características operativas. Sin embargo, si tenemos acceso a la desviación estándar y la media de la distribución del tiempo de servicio, podemos derivar la fórmula para Lq a partir de la siguiente ecuación. La distribución de llegadas en este escenario sigue la distribución exponencial negativa, concretamente en el caso de que exista un solo canal. Este escenario se conoce como caso M/G/1, que significa llegadas tipo Markov, tiempo de servicio general y un canal de servicio.
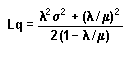
Al usar Lq, podemos determinar el valor numérico de L a través de la siguiente ecuación.
De manera similar a las propiedades operativas de los modelos M/M/1 y M/S/1, tenemos la capacidad de determinar la duración proyectada del tiempo que un individuo pasará en el sistema de línea de espera (W), así como el tiempo transcurrido. antes de ser atendido (Wq). Estas estimaciones se pueden calcular mediante la utilización de las siguientes ecuaciones.
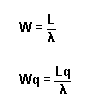
El sistema de línea de espera que se describe aquí es uno en el que los clientes llegan al azar, el tiempo de servicio para cada cliente es constante y solo hay una línea de servicio y una línea de espera. Este escenario puede verse como un caso especial del modelo M/G/1, analizado previamente, donde la desviación estándar es cero. Esto significa que, en este caso particular, es posible determinar el número exacto de clientes en la cola de espera en un momento dado.
Unidades (Lq) en espera de servicio por ecuación:
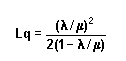
El valor de Lq puede ayudarnos a determinar todas las demás características operativas. Al utilizar Lq, podemos calcular el valor de L empleando la siguiente ecuación.
Mismas características operativas que los modelos M/M/1 y M/S/1, Podemos calcular el tiempo esperado (W) del sistema de colas, y El tiempo transcurrido antes de ser atendido (Wq), lo podemos hacer mediante Por la siguiente ecuación:
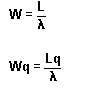
El reciente aumento en el negocio de la compañía ha resultado en la necesidad de que la secretaria maneje un mayor volumen de órdenes de compra. En promedio, debe enviar 20 órdenes de compra por día. Para procesar eficientemente estos pedidos, la secretaria dedica un promedio de 20 minutos a cada pedido, completando todo el procedimiento de carga en su computadora. Esto le permite entregar los pedidos a los proveedores. Cabe señalar que el tiempo necesario para el procedimiento de carga sigue una distribución exponencial. La secretaria trabaja en un turno estándar de ocho horas todos los días, lo que garantiza que los pedidos se envíen correctamente dentro del plazo asignado.
La cantidad de tiempo que le toma al secretario completar una OC se puede determinar de la siguiente manera.
Si quieres saber la probabilidad de que haya 5 o más secretarias. Su OC pendiente se determina de la siguiente manera:
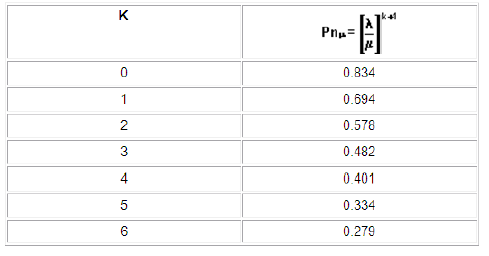
La tarea que nos ocupa es asignar una enfermera para que trabaje en una sala de primeros auxilios de un municipio. El deber principal de la enfermera será administrar vacunas contra la gripe a las personas mayores y a la población en riesgo. La enfermera tiene capacidad para vacunar a una persona cada tres minutos. A lo largo del día, se espera que los individuos lleguen a la habitación de manera independiente y aleatoria, y la tasa de llegada sigue una distribución de Poisson. Esto significa que las personas pueden llegar a un ritmo de una persona cada seis minutos, en promedio, el tiempo que tarda la enfermera en administrar cada vacuna sigue una distribución exponencial.
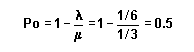
La cantidad de tiempo que el médico está ocupado o realizando tareas
El recuento general de personas que actualmente reciben y prevén recibir la vacuna covid-19.
La cantidad típica de personas que esperan en fila para recibir su vacuna.
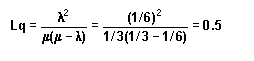
En este escenario, tenemos un call center que recibe llamadas de una oficina de reclamos de servicios públicos. Estas llamadas llegan a un ritmo de dos por minuto y se necesitan aproximadamente 20 segundos para atender cada llamada. En la actualidad, sólo hay un operador de conmutación que se ocupa de todas las llamadas entrantes. Las distribuciones de Poisson y exponencial parecen ser aplicables para analizar y comprender los patrones y características de la llegada y el manejo de llamadas en este contexto.
La cantidad de llamadas telefónicas que se encuentran actualmente en espera, esperando ser atendidas.
Durante el inicio de la temporada de fútbol, las taquillas del club de fútbol experimentan un importante aumento de actividad, especialmente el día previo al partido inaugural. Hay una afluencia constante de fanáticos, con cuatro personas que llegan cada 10 minutos, buscando ansiosamente sus entradas para el fútbol. El proceso de compra de estos billetes suele requerir un tiempo medio de dos minutos para completar cada transacción.
Electronics Corporation ha establecido un departamento de servicio de reparación para manejar las fallas de funcionamiento de las máquinas que ocurren en un promedio de tres veces al día. Se sabe que estas averías siguen un patrón de distribución de Poisson. El equipo de servicio tiene capacidad para atender una media de ocho máquinas al día y el tiempo necesario para repararlas sigue una distribución exponencial.
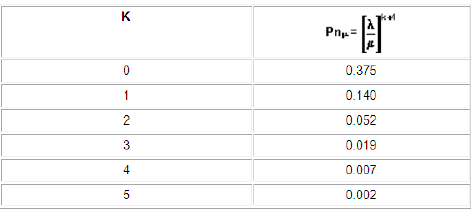
Mardel Car Wash opera un servicio de lavandería automático seis días a la semana, siendo el sábado el día de mayor actividad comercial. Basándose en registros anteriores, la empresa ha observado que el número de coches sucios que llegan a lavar los sábados es de aproximadamente 20 por hora. Al emplear un equipo completo en la línea de lavado de manos, la empresa estima que pueden lavar un automóvil cada dos minutos. En este escenario, el lavado de autos opera con una fila de espera simple, lo que significa que solo se lava un auto a la vez. Se supone que la llegada de automóviles sigue una distribución de Poisson y el tiempo necesario para lavar cada automóvil sigue una distribución exponencial.
Suéteres del Mar, una fábrica de tejidos ubicada en Mar del Plata, opera una gran cantidad de máquinas de tejer que frecuentemente encuentran problemas. Estas máquinas se reparan mediante el procedimiento primero en entrar, primero en salir (FIFO), en el que participa un equipo de 7 miembros del personal de reparación. El director de producción ha observado durante varias inspecciones que normalmente hay entre 10 y 12 máquinas fuera de funcionamiento en un momento dado debido a paradas. Al reconocer el potencial de aumentar la producción al reducir el número de máquinas inactivas, el gerente está considerando contratar personal de reparación adicional, determinar el número exacto de personas a contratar sigue siendo un desafío. El gerente está ansioso por encontrar el número óptimo de nuevas contrataciones que minimice efectivamente el tiempo de inactividad de la máquina y maximice la productividad.
3.9 Modelo y análisis del Sistema de Cola Actual.
Con base en estas observaciones, el sistema actual se puede modelar efectivamente como un sistema de colas M/M/7, con una tasa de llegada de 25 máquinas por hora, una tasa de reparación de cuatro máquinas por hora por cada servidor, una población única de máquinas y una zona de espera infinita. El primer paso que hay que dar es analizar exhaustivamente las condiciones operativas actuales. Es importante comprender que las máquinas de tejer pueden verse como colas, donde ocasionalmente se atascan y requieren reparación. Dado que existe un número significativo de máquinas de este tipo, es razonable suponer que la población de clientes es infinita. Hay un total de siete servidores independientes e idénticos encargados de reparar las máquinas, siguiendo una estrategia de primero en entrar, primero en salir. Uno puede imaginarse a estas máquinas formando una sola línea, esperando pacientemente a ser atendidas por el siguiente servidor disponible.
Tabla 3.1
Rendimiento obtenidas con Queuing Analysis „ en el WinQSB .
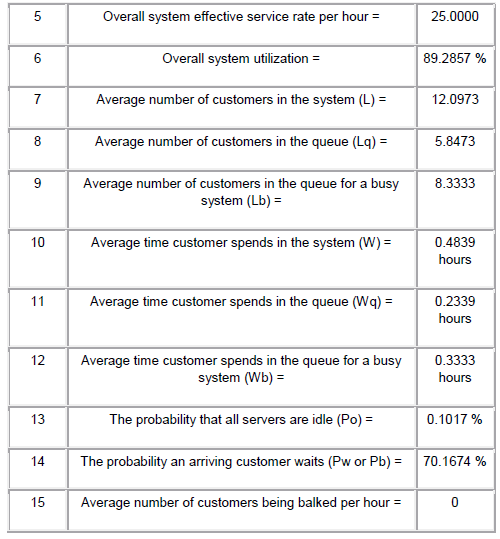
Dada esta información, resulta imperativo determinar el número de reparadores adicionales que deberían emplearse. Afortunadamente ya se conocen las medidas de desempeño de un total de 7 trabajadores. Al examinarlo, resulta evidente que la estimación del gerente de producción con respecto al número promedio de máquinas atascadas entre 10 y 12 es bastante precisa. De hecho, el informe indica que este número concretamente es el 12.09. Además, la línea 10 del informe revela que estas máquinas atascadas permanecen fuera de funcionamiento por un tiempo promedio de aproximadamente 0,4839 horas, lo que equivale aproximadamente a 29 minutos.
Para determinar si se deben contratar reparadores adicionales o no, es necesario considerar la información de costos. Las medidas de desempeño para un rango de 7 a 11 empleados de reparación se pueden encontrar en la tabla 3.2. A medida que el número de reparadores aumenta de 7 a 11, se produce una notable disminución en el número medio de máquinas que no funcionan correctamente. En concreto, el número medio de máquinas fuera de funcionamiento disminuye desde unas 12 hasta un descenso significativo de 6.333. Además, el tiempo medio que una máquina permanece fuera de funcionamiento también disminuye a medida que aumenta el tamaño del personal. Inicialmente, el tiempo medio que una máquina está fuera de funcionamiento es de aproximadamente 0,4839 horas, lo que equivale a unos 29 minutos, con el aumento del personal de reparación, este tiempo promedio disminuye a 0,2533 horas, o aproximadamente 15 minutos.
Tabla 3.2
Evaluación del Rendimiento
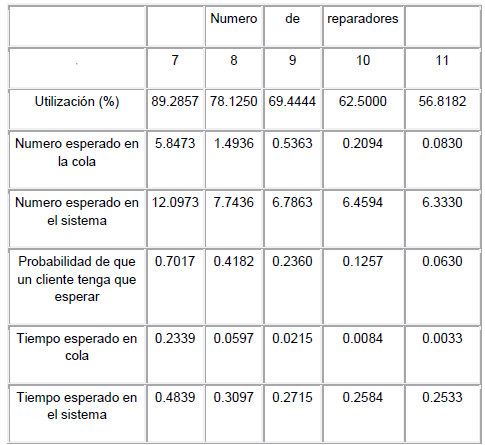
El costo total se puede determinar sumando el costo de personal y el costo de espera, esto incluye el costo por hora de cada reparador multiplicado por el número de reparadores y el costo por hora de cada máquina fuera de funcionamiento multiplicado por el número promedio de máquinas en espera de reparación. Para el ejemplo dado, el cálculo sería: (50 * 7) + (100 * 12,0973) = $1559,73 por hora. A la hora de evaluar las ventajas de emplear más personal de reparación dentro de la empresa, es fundamental tener en cuenta dos factores clave. En primer lugar, es necesario determinar el coste por hora en función del tamaño del personal. En segundo lugar, se debe calcular el costo total del número de reparaciones que cada personal puede realizar por hora y el costo por hora de cada máquina fuera de operación. Para proceder, requerimos el costo por hora de cada miembro del personal de reparación (Cs) y el costo por hora de una máquina fuera de operación (Ce), que representa la pérdida monetaria incurrida debido a una hora de producción parada. Esto incluye costos explícitos como ganancias no realizadas y costos implícitos como la posible insatisfacción del cliente causada por el incumplimiento de los plazos de entrega. Al realizar cálculos similares para cada tamaño de personal alternativo, podemos obtener los costos por hora para cada opción como se presenta en la tabla. De estos resultados se desprende que la alternativa con menor costo por hora, que asciende a $1128.63, es tener un total de 9 reparadores.
Por lo tanto, la recomendación a la dirección de producción es contratar dos reparadores adicionales. Aunque esto generará un costo adicional de $100 por hora, los ahorros logrados al tener menos máquinas fuera de operación justifican con creces este gasto. La recomendación reducirá el costo por hora de $1,559.73 a $1,128.63, lo que resultará en un ahorro de aproximadamente $430 por hora, lo que excede el costo de contratar nuevos empleados. Suponiendo que el departamento de contabilidad revela que cada mecánico de reparación le cuesta a la empresa $50 por hora, incluidos impuestos y beneficios, y estima una pérdida de $100 por cada hora que una máquina permanece inactiva, ahora podemos calcular el costo total para diferentes tamaños de personal. Por ejemplo, con una plantilla de 7 reparadores, el número esperado de máquinas en funcionamiento es 12,0973.
Para proporcionar una evaluación integral de un sistema de colas en el que se tiene la capacidad de manipular la cantidad de servidores o su tasa de servicio, es necesario considerar varias estimaciones de costos y medidas de rendimiento. Estos incluyen el costo incurrido por servidor durante un período de tiempo específico (denominado Cs), el costo acumulado por unidad de tiempo para cada cliente que espera en el sistema (conocido como Ce) y el número promedio de clientes presentes en el sistema en ese momento. en cualquier momento dado (denominado L).
CAPÍTULO IV
LAS CADENAS DE MARKOV
4.LOS MODELOS DE MARKOV
En nuestro análisis, nos centraremos principalmente en los procesos markoviano que se adhieren a los siguientes supuestos: en primer lugar, que existe un número finito y limitado de estados potenciales; en segundo lugar, que la probabilidad de transiciones de estados permanezca constante en el tiempo; en tercer lugar, que los estados futuros pueden predecirse basándose en el estado anterior y la matriz de probabilidad de transición; y finalmente, que el tamaño del sistema se mantenga constante durante todo el análisis. Estos procesos se conocen como cadenas de Markov de probabilidad de transición estacionaria y, a menudo, se denominan sin memoria. Nuestro análisis girará en torno a evaluar la probabilidad de que un cliente seleccione una tienda durante un período particular. Para facilitar nuestros cálculos, supongamos que poseemos datos de 100 compradores durante un período de 10 semanas.
Los modelos de Markov resultan muy beneficiosos al examinar la progresión de sistemas mediante ensayos repetidos. Durante cada período sucesivo de pruebas, resulta imposible determinar el resultado exacto o el estado del sistema, por lo que es necesario el uso de probabilidades de transición para describir su comportamiento. Este ejemplo también nos permite profundizar en el examen de la cuota de mercado y la fidelidad de los clientes hacia las marcas M y A. Por simplicidad, nos referiremos a los periodos semanales o visitas a tienda como "ensayos de proceso". En cada prueba, el cliente realizará una compra en M o A. A los efectos de esta discusión, no nos aventuraremos más allá de estos casos específicos y nos concentraremos principalmente en emplear software para abordar estos problemas de manera efectiva.
Para ilustrar la aplicación práctica de los modelos de Markov, consideremos un escenario de análisis de mercado. Nuestro objetivo será determinar la probabilidad de que un consumidor compre una marca en particular, etiquetada como M, en un momento dado, seguida de su compra posterior de otra marca, denominada A. Alternativamente, podemos explorar la posibilidad de que compre en la tienda. M y luego hacer la transición a la tienda A. En los procesos de Markov, la probabilidad de seleccionar una tienda en un período determinado se determina únicamente considerando la tienda elegida en el período anterior. Al emplear estos conocimientos, podemos analizar y sacar conclusiones sobre el comportamiento del cliente, la dinámica del mercado y la participación de mercado relativa entre las marcas M y A.
Una forma de representar visualmente esta información es organizándola en una matriz.
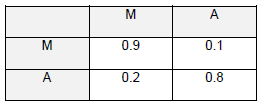
La matriz de probabilidades de transición, a la que nos referiremos como tabla, debe tener la propiedad de que la suma de cada fila sea igual a 1. Es importante tener en cuenta que este proceso supone que las probabilidades de transición permanecerán consistentes para todos los clientes y no variarán. con el tiempo.
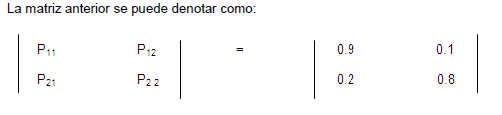
La matriz muestra la probabilidad de pasar de un estado a otro en un período de tiempo específico. Podemos observar esto analizando las entradas de la matriz.
Supongamos que comenzamos con un escenario en el que la compra más reciente de un cliente fue en la ubicación M. Para determinar la probabilidad de que este cliente realice una compra en la ubicación M en el período siguiente, necesitamos calcular la probabilidad. Alternativamente, también podemos determinar la probabilidad de que el sistema esté en la ubicación 1 después de la transición inicial.
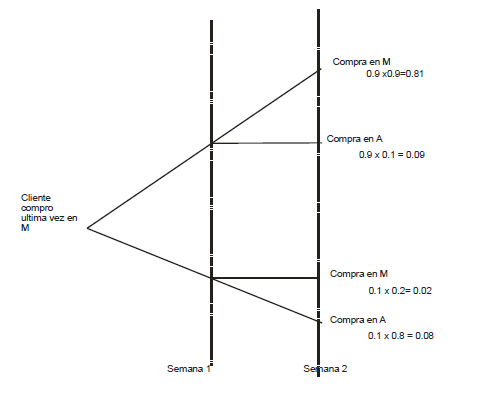
Con base en la información proporcionada, podemos determinar la probabilidad de que el cliente esté en M durante el segundo período.
Figura 4.1
Resolución con el WIN QSB
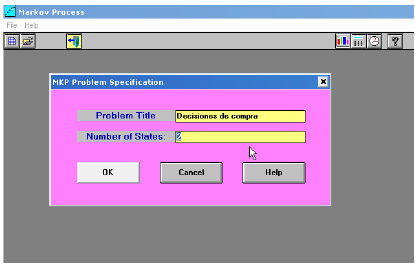
La opción Nuevo problema proporciona una plantilla completa para que los usuarios especifiquen los detalles de su problema, incluido el título del problema, el número de estados y las probabilidades y costos relevantes. Esta plantilla se puede utilizar para analizar y resolver el problema dado utilizando las opciones de menú disponibles.
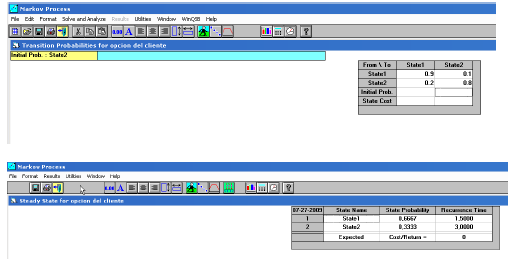
La matriz final representa las probabilidades de que el sistema alcance un estado estable. Esto implica que durante un período prolongado, habrá un 66,6% de posibilidades de que el sistema esté en el estado uno, mientras que el estado dos representará el 33,3% del tiempo.
4.1 La Administración de Proyectos.
La gestión de proyectos se puede definir como el arte de planificar, dirigir y controlar los recursos para cumplir con las limitaciones impuestas por el proyecto. Es importante señalar que cada proyecto es único y tiene un resultado final distinto. Una vez completadas las tareas, el proyecto concluye y el equipo de trabajo pasa a otras actividades. Esto contrasta con los procesos lineales e intermitentes, donde el ciclo de producción continúa o el equipo regresa a las tareas rutinarias, comprender las relaciones entre actividades es esencial para crear un diagrama de precedencia, que representa la secuencia en la que se debe llevar a cabo el proyecto. Este diagrama nos aclara qué actividades deben completarse antes de que otras puedan comenzar, al describir las tareas o actividades dentro de un proyecto, la claridad es crucial.
El equipo de planificación desempeña un papel fundamental a la hora de garantizar que la descripción sea lo suficientemente detallada para el análisis y, al mismo tiempo, evitar una granularidad excesiva que podría dificultar la comprensión. En el pasado, existían algunas diferencias metodológicas entre PERT y CPM, particularmente en términos de tiempo y tratamiento de costos. Sin embargo, hoy en día, cuando nos referimos a estas técnicas, generalmente las entendemos como diagramas de red genéricos. Los proyectos, en general, involucran una serie de actividades que necesitan ser monitoreadas cuidadosamente en términos de sus fechas de inicio y duración. A lo largo de este capítulo, nuestro objetivo es explorar varios métodos de programación y control que se pueden aplicar a este tipo específico de proceso.
Los administradores, en general, deben coordinar y gestionar proyectos dentro de los presupuestos y previsiones asignados. Se esfuerzan por evitar retrasos reasignando tareas y recursos constantemente, lo que a veces puede requerir cambios en las fechas de finalización. Para ayudar en estos esfuerzos, se han desarrollado modelos de planificación de redes. Estos modelos dividen todo el proyecto en una lista de tareas o actividades. Si bien las técnicas de diagramas de Gantt se han aplicado tradicionalmente a proyectos debido a su simplicidad, no siempre son adecuadas para proyectos complejos que requieren un mayor nivel de detalle y tienen plazos más largos. En el ámbito de los proyectos, a menudo tratamos con personal que proviene de diferentes orígenes y posee diversas habilidades.
Es probable que algunas personas sólo participen en determinadas fases del proyecto, esta característica única de la producción de proyectos presenta desafíos importantes, no sólo en términos de coordinación y control sino también en la gestión de personal. Los proyectos complejos se caracterizan por la multitud de operaciones o actividades involucradas. Métodos como CPM y PERT tienen como objetivo identificar estas actividades, establecer relaciones de red, calcular los cronogramas del proyecto y facilitar el seguimiento del progreso. La técnica de evaluación y revisión de programas (PERT) se desarrolló a finales de la década de 1950 para el programa Polaris, mientras que el método de ruta crítica (CPM) fue introducido en 1957 por las empresas Remington Rand y DuPont. Ambas técnicas emplean diagramas de red para ilustrar el flujo secuencial y las interrelaciones entre actividades. En este capítulo nos adentraremos en el mundo de los métodos de análisis de proyectos, centrándonos concretamente en las técnicas de planificación y programación conocidas como Ruta Crítica y PERT. El contenido que estás a punto de leer ha sido extraído del reconocido trabajo “Administración de Producción y Operaciones” de Carro, R y González Gómez, D.
4.2 Diagrama de Redes.
El paso inicial para crear un diagrama de red es dividir el proyecto total en una lista completa de tareas o actividades. Estas actividades individuales representan las unidades de producción más pequeñas que pueden programarse eficazmente. Dependiendo del nivel de detalle deseado, las actividades se pueden agrupar o dividir en tareas más simples. Este desglose permite una mejor planificación, asignación de recursos y seguimiento del progreso a lo largo del ciclo de vida del proyecto, los diagramas de red resaltan las actividades críticas que deben ejecutarse dentro del cronograma designado para evitar retrasos. Al identificar estas actividades críticas, los gerentes de proyectos pueden priorizarlas y asignar recursos en consecuencia, minimizando el riesgo de retrasarse. Por otro lado, las actividades no críticas pueden retrasarse hasta cierto punto sin afectar el cronograma general del proyecto.
Esta flexibilidad permite una mejor gestión y optimización de los recursos. Los diagramas de red desempeñan un papel crucial en la toma de decisiones, ya que proporcionan respuestas a varias preguntas importantes. En primer lugar, ayudan a determinar el tiempo total necesario para completar un proyecto. Esto es esencial para planificar y asignar recursos de manera eficiente, los diagramas de red brindan información valiosa sobre las fechas de inicio y finalización programadas para cada actividad. Esta información permite a los gerentes de proyectos coordinar tareas de manera efectiva y garantizar un progreso fluido. Para aplicar las técnicas PERT-CPM de forma eficaz, los proyectos deben poseer características específicas. En primer lugar, las tareas o puestos de trabajo deben definirse con precisión, sin dejar lugar a ambigüedades.
Cada tarea debe ser independiente y realizarse por separado en una secuencia predeterminada, las tareas dentro del proyecto deben seguir un orden de precedencia específico para garantizar una ejecución fluida y minimizar los conflictos. Es importante señalar que existen dos convenciones para representar diagramas de red: actividad en el arco (AOA) y actividad en el nodo (AON). En AOA, las actividades se representan en los arcos del gráfico, mientras que AON representa actividades en los nodos, y los arcos indican las relaciones entre ellos. Ambas convenciones tienen sus ventajas y pueden utilizarse según los requisitos específicos del proyecto.
Diagrama 4.1
Diagrama de Arco
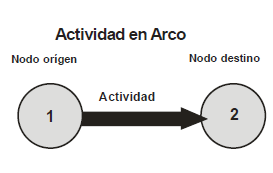
La red está compuesta de nodos, denominados eventos, sucesos o etapas, que representan puntos donde culminan las actividades y comienzan otras nuevas. Estos nodos y arcos crean una representación gráfica, conocida como diagrama de red, que ilustra las relaciones establecidas por el diagrama de precedencia. Este diagrama es esencial para cualquier proyecto que utilice técnicas de análisis de red, hay dos variaciones del diagrama: una asocia actividades con nodos, mientras que la otra las asocia con arcos. Cada actividad está representada por un arco en la red, siendo su origen y destino dos nodos diferentes, estos nodos son parte de los estados de ejecución del proyecto y comúnmente se denominan eventos.
Diagrama 4.2
Actividades en los Nodos.
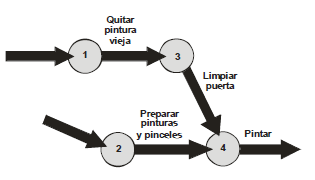
El diagrama ilustra el desglose de un proyecto en tareas individuales, que representan las unidades más pequeñas que se pueden programar. Dependiendo del nivel de detalle requerido, se pueden agrupar o subdividir varias tareas. En el diagrama, el nodo 4 representa la etapa posterior a la limpieza de la puerta, la preparación de la pintura y los pinceles, y antes de que comience el proceso de pintura real. En el sistema AOA, a veces es necesario incluir actividades ficticias para definir claramente el orden en el que se deben completar determinadas tareas. Estas tareas ficticias no tienen duración y no requieren ningún recurso. Están representados por líneas de puntos en el diagrama. Este enfoque también se utiliza cuando dos actividades tienen el mismo punto inicial y final.
Diagrama 4.3
Ejemplo:
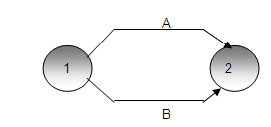La actividad 1 y 2 debe ser única.
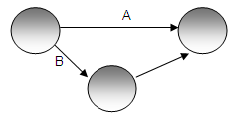
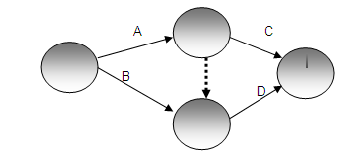
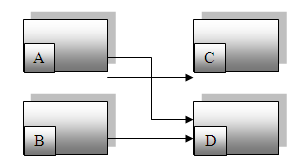
Uno de los principales beneficios de utilizar el formato Actividades en el nodo (AON) es la eliminación de la necesidad de actividades ficticias. Para ilustrar mejor esta ventaja, consideremos otro escenario. Imaginemos que estamos emprendiendo un proyecto que implica pintar varias habitaciones. En este proyecto en particular, tenemos la tarea de pintar tres habitaciones separadas, y cada habitación requiere una secuencia específica de actividades. Estas actividades incluyen preparar la habitación, pintar el techo y las paredes y, en última instancia, completar el proceso de decoración
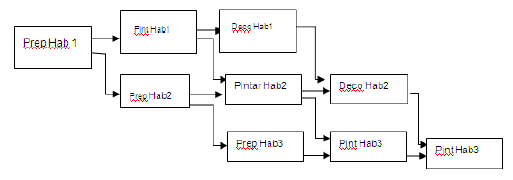
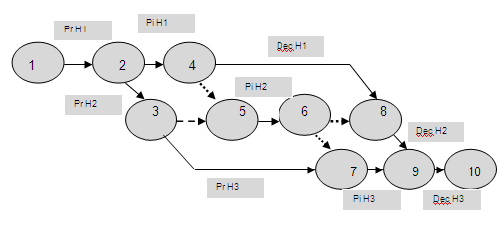
Las técnicas PERT y CPM se centran principalmente en analizar y determinar el tiempo necesario para la finalización del proyecto. Al utilizar diagramas de red y varios cálculos, los gerentes de proyectos pueden identificar el camino crítico y establecer fechas importantes para cada actividad. La notación utilizada en estas técnicas ayuda a resolver la red y comprender el momento de las tareas individuales, la disponibilidad de datos históricos puede proporcionar información valiosa y certeza en la programación de proyectos, mientras que los nuevos proyectos pueden enfrentar incertidumbres y riesgos. Cuando un proyecto tiene antecedentes históricos, es decir, se han ejecutado proyectos similares en el pasado, el director del proyecto posee información precisa y un alto nivel de certeza sobre el calendario de las tareas individuales, si el proyecto es completamente nuevo, sin comparaciones o experiencias previas, el director del proyecto tendrá que afrontar riesgos e incertidumbres.
Después de crear un diagrama de red para representar el proyecto, resulta más fácil calcular fechas importantes para cada actividad, como las horas de inicio y finalización más tempranas. Suponiendo que el proyecto comienza en la fecha cero (que puede representar cualquier otra fecha cronológica de inicio), se determinan diferentes horas de inicio y finalización para cada actividad y para todo el proyecto estos cálculos se realizan utilizando la notación AOA (Actividad en flecha) universalmente aceptada.
La ruta crítica se refiere a la ruta en una red que tarda más tiempo en recorrerse. Es crucial porque determina la fecha final de finalización del proyecto. Cualquier retraso en las actividades a lo largo de este camino resultará en un retraso para todo el proyecto.
Si bien los programas informáticos se utilizan normalmente para el análisis de redes, es beneficioso proporcionar una explicación detallada del procedimiento y su importancia práctica. Para comprender mejor el modelo, consideremos un ejemplo sencillo que emplea la metodología AOA. Imaginemos un proyecto básico en el que estamos diseñando un programa informático con fines de construcción. Para ilustrar mejor el concepto, presentaremos una tabla que describe una serie de actividades o tareas, junto con sus dependencias y duraciones, que generalmente se derivan de los sectores técnicos.
Durante los dos pasos por la red, se calculan las fechas más tempranas y las fechas límite para cada nodo. El proceso de cálculo es el siguiente: en la primera pasada, al nodo inicial se le asigna un valor de 0. Luego, para cada actividad que se origina en el nodo previamente calculado, se toma el valor de la fecha de inicio más temprana (ES) más la duración del Se calcula la actividad (D). Si el nodo destino de la actividad aún no tiene un valor, se asigna el valor calculado. Si el nodo de destino ya tiene un valor, pero es menor que el valor calculado, se asigna el nuevo valor, si el nodo de destino tiene un valor mayor o igual al valor calculado, no se realiza ninguna acción. La regla general para esta etapa es utilizar el valor máximo encontrado entre los diferentes caminos que conducen al nodo. Al realizar este segundo pase se determinan los últimos tiempos posibles de inicio de cada actividad en cada nodo se utiliza el valor más bajo encontrado entre los diferentes caminos que conducen a él.
Una vez que se han calculado todos los nodos, se completa la segunda pasada. Una vez que se han calculado todos los nodos con sus fechas de inicio más tempranas, se completa la primera pasada. El valor obtenido para el nodo final indica la fecha de finalización más temprana posible para todo el proyecto, teniendo en cuenta la precedencia y el calendario de todas las actividades en la red. La técnica consta de una serie de pasos que se deben seguir para poder analizar y planificar eficazmente un proyecto. Estos pasos incluyen identificar las diversas actividades involucradas, establecer la secuencia en la que deben completarse estas actividades, construir una red para visualizar y organizar el proyecto y determinar la ruta crítica.
En la segunda pasada, la atención se centra en calcular las últimas fechas posibles para cada actividad al nodo final se le asigna el valor de finalización mínimo posible para todo el proyecto. Luego, para cada actividad cuyo nodo de destino se esté evaluando, se calcula el valor del nodo de destino menos la duración de la actividad. Si el nodo origen de la actividad aún no tiene valor, se asigna el valor calculado. Si el nodo de origen ya tiene un valor, pero es mayor que el valor calculado, se asigna el nuevo valor. Si el nodo de origen tiene un valor menor o igual al valor calculado, no se realiza ninguna acción. La regla general para esta etapa es utilizar el valor mínimo encontrado entre todos los nodos sucesores inmediatos.
La fecha más temprana de un nodo significa el momento más temprano en el que se puede lograr el evento correspondiente, mientras que la fecha límite representa el último momento posible en el que debe ocurrir el evento para mantener la fecha de finalización del proyecto. Además, se introduce el concepto de holgura, que indica si un evento se completa antes de lo previsto, a tiempo o con retraso. La holgura de un nodo se calcula restando la fecha más temprana de la fecha límite, esta técnica implica un enfoque sistemático para analizar y planificar un proyecto. Siguiendo los pasos descritos, se puede determinar efectivamente la secuencia de actividades, identificar el camino crítico y establecer las fechas más tempranas y más tardías para cada evento. Esta información es crucial para una gestión exitosa del proyecto y para garantizar su finalización oportuna. Para realizar esta técnica se realizan dos pasadas por la red. El primer pase comienza desde el nodo inicial y avanza hacia el nodo final. Durante este paso, se asignan valores a cada nodo en función del momento más temprano posible en el que se pueda alcanzar. Es importante tener en cuenta que cada nodo representa una etapa o evento del proyecto y tiene dos fechas correspondientes: la fecha más temprana y la fecha límite.
El diagrama ilustra el proceso de determinar las fechas tempranas y tardías dentro de un proyecto. Esto se logra utilizando un método de dos pasos, donde el primer paso calcula las fechas tempranas atravesando la red desde el nodo inicial hasta el nodo final, y el segundo paso calcula las fechas tardías atravesando la red en la dirección opuesta. A medida que se atraviesan los nodos, se les asignan valores. Una vez que se hayan realizado todos los cálculos necesarios para determinar el momento más temprano, la fecha límite del proyecto y los tiempos de actividad, podemos identificar la ruta crítica. Los nodos críticos se definen como aquellos con fechas tempranas y tardías iguales, mientras que las tareas críticas tienen un margen total cero.
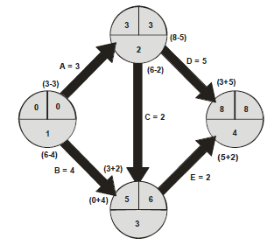
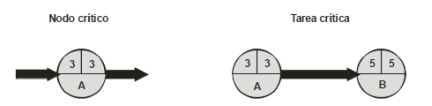
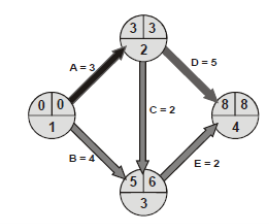
Este diagrama representa el paso final en el proceso de cálculo y muestra la red junto con los dos resultados de los nodos. Estos resultados incluyen el momento más temprano y el método de cálculo para todas las actividades del proyecto. Las actividades que componen la ruta crítica se identifican por su autorización total mínima.
ESi es igual a LSi. Estos eventos en particular son cruciales porque tienen los mismos horarios de inicio más cercanos posibles. Se ha observado que los eventos 1, 2 y 4 son críticos porque su ES (Earliest Start) es igual a su LS (Latest Start), formando así la ruta crítica del proyecto, que consta de los eventos 1, 2 y 4. En un proyecto típico, que puede constar de cientos de actividades, sólo un pequeño porcentaje (alrededor del 5 al 10%) de estas actividades se considera parte de la ruta crítica, en el análisis de redes, se puede calcular el margen de un evento. Esto permite identificar actividades que no se encuentran en la ruta crítica pero que pueden experimentar algunos retrasos, denominados margen, sin afectar el tiempo general de finalización del proyecto. Como se explicó anteriormente, el margen es la cantidad máxima de holgura que se puede permitir en cualquier camino determinado. el margen para una ruta particular se puede calcular restando la longitud de esa ruta de la longitud de la ruta crítica.
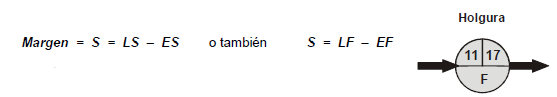
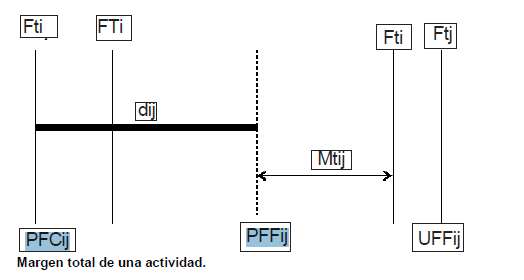
Para decirlo de otra manera, la ruta crítica es la duración en la que se puede completar una actividad sin causar ningún retraso en el cronograma general del proyecto. Los eventos de ruta crítica no tienen tiempo de holgura. Por otro lado, el Margen Total de una actividad significa la cantidad máxima de tiempo que se puede posponer sin afectar el cronograma del proyecto. En otras palabras, si una actividad supera su Margen General, se vuelve crítica y el proyecto enfrentará retrasos.
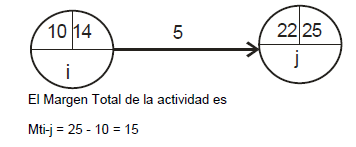
Esto implica que si la tarea toma 20 unidades de tiempo (lo que hace que la duración total sea de 25 unidades en lugar de las 5 originales), el nodo inicial tendría una Fecha temprana de 10 y el nodo final tendría una Fecha tardía de 25, como se muestra en la ilustración a continuación. Utilizar el margen total para planificar una actividad implicaría hacer que la actividad sea crucial y coordinar las tareas de una rama que se alinea con el evento i y las tareas de una rama que se origina en el evento j.
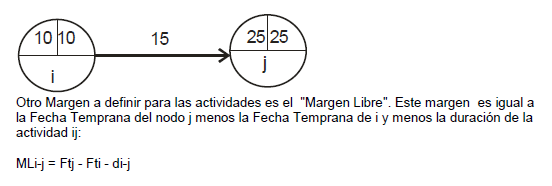
Diagrama 4.4
El Margen Libre
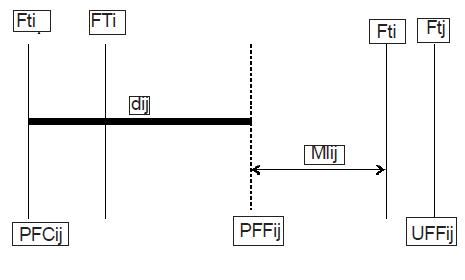
Este concepto es particularmente útil cuando es necesario que un proyecto comience lo antes posible sin realizar ningún cambio en las fechas temprana y tardía de un nodo específico, conocido como nodo j. Volviendo al ejemplo proporcionado en la figura, el margen libre se puede calcular restando la fecha temprana (10) y la fecha tardía (5) del nodo j de la duración total (22), lo que da como resultado un valor de margen libre de 7. Esto significa que si la tarea se extendiera en 7 unidades de tiempo (haciendo que la duración total fuera de 12 unidades en lugar de las 5 originales) y se programara su inicio en su fecha temprana (10), no afectaría las fechas tempranas y tardías de evento j. Esto se ilustra en la siguiente figura. Al utilizar el enfoque de margen libre, programar una actividad de esta manera hace que el nodo de origen sea crítico, lo que esencialmente requiere un compromiso hacia atrás con el proyecto, mientras se deja inalterada la progresión hacia adelante del proyecto.
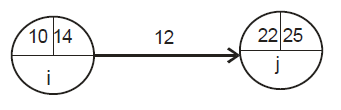
El "Margen Independiente" de una actividad se refiere a la diferencia entre la Fecha Temprana de un nodo específico y la suma de la Fecha Tardía de ese nodo junto con la duración de la tarea.
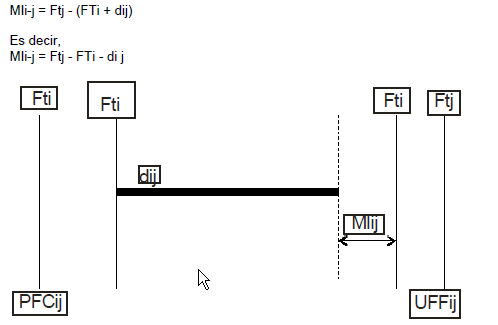
El margen independiente representa el margen total disponible para la planificación. Actividad sin cambiar los bordes de los nodos de origen y final de la actividad. Esto significa que si se agota todo el alcance, el proyecto ni siquiera se comprometerá hacia atrás. Nodo i antes del nodo j. En el mismo ejemplo, el margen independiente es:
Esto significa que incluso si la actividad está programada para comenzar en su Fecha Tardía, el margen del evento i seguiría siendo 4 y el margen del evento j seguiría siendo 3, como se muestra en la Figura. Si el Margen Independiente es negativo, significa que no es posible programar la actividad para que comience en la Fecha Tardía de i y la Fecha Temprana de j permanezca sin cambios. Por ejemplo, si la duración de la tarea ij fuera de 10 unidades, el Margen Independiente sería.
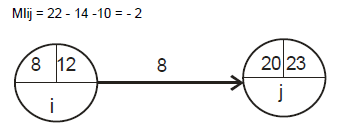
Para mantener los márgenes de ambos nodos i y j en sus niveles actuales, es necesario ajustar la duración de la actividad de 10 a 8 unidades. La ruta crítica consta de nodos que tienen la misma fecha tardía que su fecha temprana, y las actividades críticas dentro de esta ruta deben tener un margen total de cero. Es importante señalar que la presencia de dos nodos críticos no siempre indica criticidad para la actividad, es fundamental verificar que el MT (Tiempo de margen) sea efectivamente cero.
4.2 La Situación Probabilística.
Para analizar con precisión estos temas, es esencial tener información detallada sobre la distribución de probabilidad y la duración de cada actividad del proyecto, en términos prácticos, suele resultar poco práctico obtener información tan detallada para cada actividad, especialmente en proyectos con cientos o miles de tareas. En cambio, se utilizan aproximaciones a distribuciones probabilísticas teóricas, donde las distribuciones reales (subjetivas) se aproximan seleccionando ciertos parámetros. Un modelo probabilístico comúnmente utilizado en el análisis de redes es la distribución Beta, denotada como β. Esta distribución especifica las duraciones optimista, pesimista y más probable para cada tarea.
La distribución Beta ha encontrado aplicaciones en diversos problemas económicos, como la lealtad a la marca, el análisis de inversiones y la valoración. Hasta ahora se ha asumido comúnmente que las tareas de un proyecto tienen una duración fija que se conoce con certeza. Por ejemplo, inicialmente se estimó que la actividad de "diseño general" para el proyecto de ilustración duraría 3 días, en escenarios prácticos, los datos rara vez son tan predecibles. La duración de una tarea puede variar y, en el caso de la actividad de "diseño general", podría tardar entre 2 y 5 días. Sin embargo, se considera que los métodos probabilísticos están más alineados con la realidad. Estos métodos reconocen que cada actividad puede tener un rango de duraciones posibles y asignan una probabilidad a cada una de estas duraciones. Por ejemplo, se podría estimar que la actividad de "diseño general" mencionada anteriormente tiene una duración planificada que oscila entre 1 y 6 días, con una distribución probabilística específica. Al realizar un análisis probabilístico de las actividades del proyecto, un gerente obtiene información valiosa para la toma de decisiones. Pueden responder preguntas cruciales como la probabilidad de que una actividad se retrase más allá de una fecha determinada, la probabilidad de que el proyecto no se complete en una fecha límite específica y las posibilidades de que una actividad crítica afecte la duración general del proyecto. Para abordar esta incertidumbre, se han utilizado métodos deterministas como el Diagrama de Grantt o el Diagrama de Necesidades, estos métodos reemplazan el rango de valores posibles con el valor esperado, que representa la duración promedio de la tarea.
La duración de un trabajo complejo puede variar mucho dependiendo de varios factores, incluida su capacidad de adaptarse a diferentes situaciones. La distribución uniforme o distribución rectangular es un tipo específico de distribución beta. Esta distribución también puede dar lugar a distribuciones triangulares, distribuciones parabólicas e incluso una densidad tipo bañera. El tiempo optimista es el periodo más corto en el que se puede completar la actividad si todo va según lo previsto. El tiempo pesimista, por su parte, es la duración máxima estimada para la actividad en condiciones adversas ordinarias. Se supone que sólo hay una probabilidad entre cien de completar la actividad antes del tiempo optimista o exceder el tiempo pesimista.
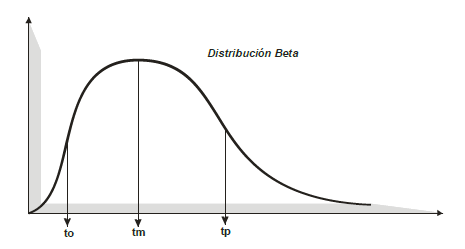
Al aplicar estos conceptos a la actividad de "diseño general", en lugar de asumir una duración fija de tres días, especificaremos tres valores: to = 1, tp = 6 y m = 3. Estos valores nos permitirán ajustar un Beta distribución para representar la distribución de probabilidad de la duración de la actividad. Para crear este modelo probabilístico, utilizaremos conocimientos de la teoría de la probabilidad y la estadística
El valor medio de una variable que sigue una distribución Beta se puede determinar utilizando la fórmula del valor esperado.
La varianza de la distribución Beta se puede determinar mediante un cálculo específico.
La varianza de la suma de variables aleatorias independientes se encuentra simplemente sumando las varianzas de cada variable individual. Hay algunos autores, como Sasieni en 1986, que sostienen que no es posible justificar rigurosamente el uso de la distribución Beta, sin embargo, para los propósitos de esta discusión, aceptemos que la distribución Beta se caracteriza por ser unimodal, continua y tener un intervalo finito. Al tratarse de una gran cantidad de variables aleatorias, mayor a 30, se observa que la suma de sus valores sigue una distribución aleatoria conocida como distribución normal. Esta distribución tiene un valor medio que es igual a la suma de los valores medios de las variables individuales. Sorprendentemente, esto es cierto incluso si las variables individuales no siguen una distribución normal.
4.3 Análisis de las Probabilidades.
Dada la naturaleza incierta de este análisis, es crucial que el director del proyecto determine la probabilidad de completar el proyecto dentro de un plazo específico. Una pregunta común que surge es la probabilidad de completar el proyecto en menos de 60 días. Para determinar la distribución de probabilidad del tiempo de finalización, se supone que las duraciones de cada actividad son independientes entre sí. Este supuesto nos permite calcular la media y la varianza de la distribución de probabilidad sumando los tiempos de duración y sus varianzas a lo largo del camino crítico, se aplica el teorema del límite central, que indica que a medida que aumenta el número de variables independientes, su suma se acerca a una distribución normal. En el contexto del análisis de redes, la media de la distribución normal de la ruta crítica representa el tiempo de finalización más temprano esperado del proyecto. La varianza, por otro lado, refleja el nivel de incertidumbre asociado a cada actividad. A mayor varianza, aumenta el nivel de incertidumbre, al comprender la variación de las actividades a lo largo de la ruta crítica y la variación total asociada a ella, resulta más fácil calcular las probabilidades de las fechas de terminación del proyecto. La varianza de la ruta crítica se determina sumando las variaciones de las actividades individuales a lo largo de la ruta crítica. Por lo tanto, para analizar la probabilidad de completar un proyecto en una fecha específica utilizando la distribución normal, el cálculo implica determinar la media y la varianza.
El proceso implica varios pasos, primero, se calcula la varianza para cada actividad en la ruta crítica[1]. Luego, se determina el número de desviaciones estándar (Z). Utilizando este valor, se puede consultar una tabla de probabilidad normal[2] para encontrar la probabilidad de completar el proyecto en la fecha límite deseada. Para comprender mejor estos pasos, consideremos un ejemplo. En la siguiente tabla encontrará las estimaciones optimistas, pesimistas y más probables para cada actividad.
El tiempo se mide en semanas y también se proporciona el diagrama de red. Necesitamos calcular el tiempo esperado para cada actividad, identificar la ruta crítica, determinar la duración esperada del proyecto, calcular la varianza y la desviación estándar de la ruta crítica, encontrar la actividad con el tiempo estimado más preciso y calcular la probabilidad de completar el proyecto en 20 semanas.
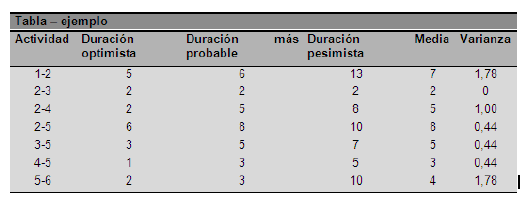
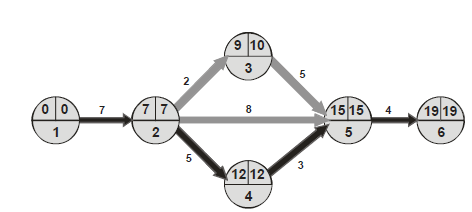
Una vez determinados los valores esperados y las varianzas de cada actividad, se representa la red utilizando los tiempos esperados. Esta representación se muestra en la figura anterior. El camino crítico, que es la secuencia de actividades con margen nulo (S = 0), se identifica como 1-2-4-5-6, la Actividad 2-5 también es crítica. Esto quiere decir que existe un doble camino crítico: 1-2-4-5-6 y 1-2-5-6. La duración esperada de la ruta crítica, Te, se calcula en 19 semanas. La varianza total de la ruta crítica se puede obtener sumando las variaciones de las actividades individuales que componen la ruta crítica.
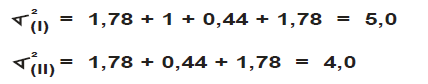
En este escenario particular, la varianza que se toma en consideración es el valor más alto entre las dos opciones, que es 5,0. La desviación estándar, por otro lado, se calcula sacando la raíz cuadrada de la varianza.
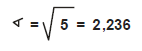
La actividad 2-3 tiene la variación más pequeña posible de todas las actividades del proyecto, que es cero. La distribución de probabilidad normal se utiliza comúnmente como estimación de la distribución de la duración del proyecto, esto nos permite calcular las probabilidades de diferentes tiempos de terminación de proyectos.
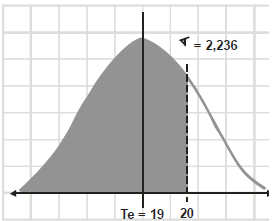
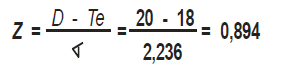
Utilizando la información proporcionada en las tablas de probabilidad normal, se calcula que el área sombreada es 0,8133. Esto implica que existe una probabilidad de 0,8133 de completar el proyecto en un lapso de 20 semanas, que también se puede expresar como 81,33%.
CONCLUSIONES
Los tomadores de decisión y administradores de empresas a menudo, luchan con graves lagunas de información, la evaluación de riesgos se utiliza para cuantificar la diferencia entre lo que se sabe y lo que se necesita para tomar disposiciones óptimas. Los modelos probabilísticos actúan como protección contra la incertidumbre adversa y la explotación de esta. La teoría de la decisión surge del concepto de funciones de utilidad de pago y, sugiere que las decisiones deben tomarse calculando los beneficios y probabilidades de diferentes opciones dentro de un cierto rango, estableciendo estrategias para una toma de decisiones efectiva. En teoría, la toma de decisiones involucra, integrar información sobre probabilidades con deseos e intereses. Este enfoque, que considera las decisiones como apuestas, subyace a la teoría de la decisión. Para hacer esto, es necesario comparar el valor de un determinado resultado con la probabilidad de que ocurra. En el campo de los modelos probabilísticos, a menudo se los compara con juegos en los que las acciones se basan en resultados esperados.
La transición de modelos deterministas a modelos probabilísticos implica el uso de métodos estadísticos subjetivos para estimación, prueba y pronóstico. En estos modelos, el riesgo se refiere a la incertidumbre con una distribución de probabilidad conocida. Por lo tanto, la evaluación de riesgos implica un examen exhaustivo para determinar las posibles consecuencias de las decisiones y sus probabilidades asociadas. Al participar en el proceso, asume el papel de sustituto de la certeza, llenando vacíos en el conocimiento completo. Los modelos probabilísticos se basan en aplicaciones estadísticas para evaluar eventos y factores incontrolables, así como evaluar los riesgos involucrados en la toma de decisiones. Originalmente, las estadísticas tenían como objetivo recopilar información para el estado, y el término en sí proviene de una palabra italiana que significa "felicidad". La probabilidad, por otro lado, tiene una historia más larga, ya que proviene del verbo "probar", que significa buscar comprensión y adquirir conocimiento.
La palabra "prueba" tiene el mismo origen y contiene los detalles necesarios para comprender lo que se cree cierto. Los problemas de toma de decisiones se ilustran aún más por la complejidad de las alternativas disponibles. Los tomadores de decisiones deben lidiar con información limitada al considerar las consecuencias de una acción y en muchos casos también deben anticipar y comparar las consecuencias de varias acciones; Además, a menudo entran en juego factores desconocidos y los resultados rara vez son claros. A menudo, el resultado depende de las reacciones de otros, que tal vez ni siquiera sean conscientes de sus propias acciones.
Por lo tanto, no es sorprendente que quienes toman decisiones a veces retrasen la toma de una decisión lo más posible o la tomen sin considerar plenamente todas las consecuencias. Cuando las personas tienen que tomar una decisión, a menudo eligen una opción sin considerar cuidadosamente todas las posibles consecuencias. La toma de decisiones implica el proceso de integrar información probabilística con los deseos e intereses de uno. Un aspecto importante de la teoría de la decisión es abordar las decisiones como si fueran apuestas, en las que las personas deben equilibrar el valor de un resultado particular con la probabilidad de que ese resultado realmente ocurra. El concepto de teoría de la decisión proviene del concepto de función de utilidad de pago, que sugiere que las decisiones deben tomarse evaluando las utilidades y probabilidades asociadas con diferentes alternativas, utilizando estrategias de priorización para una toma de decisiones efectiva, que permita a las personas navegar por la complejidad de la elección y. optimizarlo. sus resultados.
BIBLIOGRAFÍA
Anderson, Sweeney, y Williams, (1993). Introducción a los Modelos Cuantitativos para la
Administración. Grupo Editorial Iberoamericana.
Aracil,J., (1983). Introducción a la Dinámica de Sistemas, Alianza Ed.,1983.
Banks J., Carson J., Nelson B., Y Nicol D., (2001). "Discrete-Event System Simulation”,
Prentice Hall.
Bazaraa, M. y Jarvis, J.,(1976). Programación Lineal y Flujo en Redes, Limusa.
Bazaraa, M., Jarvis, J., Sherali, H., (1998). Programación Lineal y Flujo en Redes, Limusa,
Bernard P. Zeigler, Praehofer Y Tag Gon Kim. "Theory of Modeling and Simulation",
second edition, Academic Press, 2000.
Bonini, Hausman, Bierman, (1999). Análisis Cuantitativo para los Negocios. Mc Graw
Bronson, R.,(1990). Investigación de Operaciones, Serie Schaum, Mc Graw Hill.
Casti, J., (1991). Reality Rules: Picturing the World in Mathematics Vol 1 y 2, Wiley.
Casti, J., (1997). Would –be Worlds: How Simulation is Changing the Frontiers of
Science? Wiley, 1997.
casti, J.(1994). Complexification, Harper Collins.
Castillo E., Conejo A., Pedregal P., Garcia R. y Alguacil N.(2002) Formulación y
Resolución de Modelos de programación Matemática en Ingeniería y Ciencia. Centro de Documentación de la Fac. de Ciencias Económicas UNMP. //eco.mdp.edu.arCompañía Editorial continental. Coss bu "Simulación: un enfoque práctico" . Editorial Limusa.
Deaton, M &. Winebrake, J.J. Dynamic Modeling of Environmental Systems, (2000).
Springer Verlag ,
Eppen, G., Gould, F.J., SCHMIDT, C.P., Moore, Jeffrey H y Weatherford, Larry.
Investigación de Operaciones en la Ciencia Administrativa. 5º Edición.(2000). Edit Pearson. Prentice Hall
Feurzeig, W & Roberts, N., (1999). Modeling and Simulation in Science and Mathematics
Education, Springer.
Ford, A., (1999). Modeling The Environment, Island Press.
Forrester, J., (1969). Principles of Systems, Wright Allen Press.
Forrester, J., (1969). Urban Dynamics, MIT Press.
Forrester, J., (1971). World Dynamics, Wright Allen Press.
Forrester, J., (1961), Industrial Dynamics MIT Press,1961.
Goodman, M.R. (1980). Study Notes in System Dynamics, MIT Press
Graw Hill.
Hannon, B., y Ruth, M., (2001). Dynamic Modeling, 2 ed., Springer Verlag.
Hannon, B. y Ruth, M., (1997). Modeling Dynamic Economic Systems, Springer.
Hannon, B. y Ruth, M., (1997). Modeling Dynamics Biological Systems, Springer,
Hargrove J., (1998). Dynamic Modeling in The Health Sciences, Springer.
Hill, 9a. Edición.
Hillier, F. y Lieberman, G., (2003). Introducción a la Investigación de Operaciones, Mc
II. Edit Limusa. Investigación operativa. Tomos I y II.
James R., y Olson., D., (1998). Introduction to Simulation and Risk Analysis" Prentice
Hall.
Banks, J.(1998). "Handbook of Simulation. Wiley.
Martín, G., (2004). Teoría y ejercicios prácticos de Dinámica de Sistemas. Catedra
Unesco.(2007). UPC . Barcelona. España.2007.ISBN 84-607-9304-4.
Kauffman, A.(s/f). Métodos, modelos de la i.
Martínez, S., y Requena, A., (1987). Dinámica de Sistemas, , Alianza Ed..
Mathur, y Solow, (1996). Investigación de Operaciones. Prentice Hall.
Meadows, D., and D., (1992). Beyond The Limits, Chelsea G.P.
Meadows, D.H. and D.L., (1991). The Global Citizen, Island Press.
Meadows, D.H. and D.L., (1972). The Limits to Growth, Mentor.
Michael P., (1998). "Computer Simulation in Management Science" , Wiley.
Odum H.T. & E., (2000) Modeling for all Scales, Academic Press.
Pine, D., (1988). Emerging Syntheses in Science, Ed., Addison-Wesley.
Prawda, J.,(1995). Métodos y Modelos de Investigación de Operaciones. Volumen I y Vol
Render, Y Hanna.(2006).Métodos cuantitativos para los negocios.9º Edic. Pearson.
Richardson, G., (1991). Feedback Thought in Social Science and Systems Theory,
University of Pennsylvania Press.
Ross S.,(1999). "Simulación", segunda edición M. Prentice Hall.
Sterman, J., (2000). Business Dynamics: Systems Thinking and Modeling for a Complex
World, Mc-Graw Hill.
Taha, Hamdy A.(1998). Investigación de Operaciones. Una Introducción, 6º Edic. Pearson.
Incluye el software Tora.
Wayne L. Wilston."Simulation Modeling using @RISK" de Duxbury, 2001.
Wayne L. Winston Y S. Christian, A., (2001). "Practical Management Science", second
edition, de. Duxbury.
Wiener, N., (1948). Cybernetics MIT Press.
Winston, W., (1994). Investigación de Operaciones. Grupo Editorial Iberoamérica.
1